

分析 (1)结论:FG=CE,FG∥CE.如图1中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.
(2)结论仍然成立.如图2中,设DE与CF交于点M,首先证明△CBF≌△DCE,推出DE⊥CF,再证明四边形EGFC是平行四边形即可.
(3)结论仍然成立.如图3中,设DE与FC的延长线交于点M,证明方法类似.
解答 解:(1)结论:FG=CE,FG∥CE.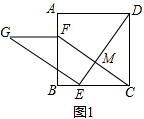
理由:如图1中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
$\left\{\begin{array}{l}{BF=CE}\\{∠CBF=∠ECD}\\{BC=CD}\end{array}\right.$,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(2)结论仍然成立.
理由:如图2中,设DE与CF交于点M.
∵四边形ABCD是正方形,
∴BC=CD,∠ABC=∠DCE=90°,
在△CBF和△DCE中,
$\left\{\begin{array}{l}{BF=CE}\\{∠CBF=∠ECD}\\{BC=CD}\end{array}\right.$,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE,
∵∠BCF+∠DCM=90°,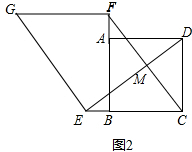
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
(3)结论仍然成立.
理由:如图3中,设DE与FC的延长线交于点M.
∵四边形ABCD是正方形,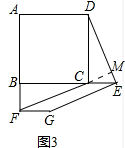
∴BC=CD,∠ABC=∠DCE=90°,
∴∠CBF=∠DCE=90°
在△CBF和△DCE中,
$\left\{\begin{array}{l}{BF=CE}\\{∠CBF=∠DCE}\\{BC=DC}\end{array}\right.$,
∴△CBF≌△DCE,
∴∠BCF=∠CDE,CF=DE
∵∠BCF+∠DCM=90°,
∴∠CDE+∠DCM=90°,
∴∠CMD=90°,
∴CF⊥DE,
∵GE⊥DE,
∴EG∥CF,
∵EG=DE,CF=DE,
∴EG=CF,
∴四边形EGFC是平行四边形.
∴GF=EC,
∴GF=EC,GF∥EC.
点评 本题考查四边形综合题、正方形的性质、平行四边形的判定和性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形,注意这类题目的解题规律,图形变了,条件不变,证明的方法思路完全一样,属于中考常考题型.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
| A. | ①②④ | B. | ①③④ | C. | ③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x<2 | C. | 1<x<2 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角互补 | |
| B. | 多边形的外角和小于内角和 | |
| C. | 平方根等于本身的数是1 | |
| D. | 同一平面内,垂直于同一条直线的两条直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )
中国数学史上最先完成勾股定理证明的数学家是公元3世纪三国时期的赵爽,他为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”(如图1).图2由弦图变化得到,它是用八个全等的直角三角形拼接而成.将图中正方形MNKT,正方形EFGH,正方形ABCD的面积分别记为S1,S2,S3,若S1+S2+S3=18,则正方形EFGH的面积为( )| A. | 9 | B. | 6 | C. | 5 | D. | $\frac{9}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com