
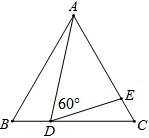
 已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.
已知:如图,△ABC是等边三角形,点D、E分别在边BC、AC上,∠ADE=60°.分析 (1)△ABC是等边三角形,得到∠B=∠C=60°,AB=AC,推出∠BAD=∠CDE,得到△ABD∽△DCE;
(2)由△ABD∽△DCE,得到$\frac{BD}{AB}$=$\frac{CE}{DC}$,然后代入数值求得结果.
解答 (1)证明:∵△ABC是等边三角形,
∴∠B=∠C=60°,AB=AC,
∵∠B+∠BAD=∠ADE+∠CDE,∠B=∠ADE=60°,
∴∠BAD=∠CDE
∴△ABD∽△DCE;
(2)解:由(1)证得△ABD∽△DCE,
∴$\frac{BD}{AB}$=$\frac{CE}{DC}$,
设CD=x,则BD=3-x,
∴$\frac{3-x}{3}$=$\frac{\frac{2}{3}}{x}$,
∴x=1或x=2,
∴DC=1或DC=2.
点评 本题考查了等边三角形的性质,相似三角形的判定和性质,注意数形结合和方程思想的应用.


 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
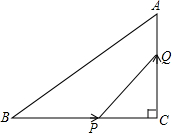 如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,同时动点Q从C出发以1cm/s的速度向点A移动,设它们的运动时间为t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.
如图,已知△ABC、△DCE、△FEG是三个全等的等腰三角形,底边BC、CE、EG在同一直线上,且AB=$\sqrt{3}$,BC=1.连接BF,分别交AC、DC、DE与点P、Q、R.有下列结论①△BFG∽△ABC、②BQ=FQ、③AP=2PC、④EF平分∠BFG,你认为不正确的是④.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
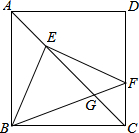 如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.
如图,已知,正方形ABCD的边长为1,点E、F分别在AC、DC上,若EC=BC,EF⊥BE,BF与EC交于G,则BG与GF的乘积为$3\sqrt{2}-4$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com