
【题目】在一个不透明的盒子里装有3个分别写有数字﹣2,0,1的小球,它们除了数字不同以外其余完全相同,先从盒子里随机抽取1个小球,再从剩下的小球中抽取1个,将这两个小球上的数字依次记为a,b,则满足关于x的方程x2+ax+b=0有实数根的概率为_____.
科目:初中数学 来源: 题型:
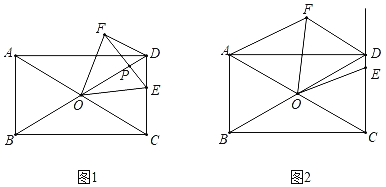
【题目】如图1,在矩形ABCD中,AB=1,对角线AC,BD相交于点O,∠COD=60°,点E是线段CD上一点,连接OE,将线段OE绕点O逆时针旋转60°得到线段OF,连接DF.
(1)求证:DF=CE;
(2)连接EF交OD于点P,求DP的最大值;
(3)如图2,点E在射线CD上运动,连接AF,在点E的运动过程中,若AF=AB,求OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)甲说:该二次函数的图象必定经过点![]() .乙说:若图象的顶点在x轴上,则
.乙说:若图象的顶点在x轴上,则![]() ,你觉得他们的结论对吗?请说明理由;
,你觉得他们的结论对吗?请说明理由;
(2)若抛物线经过![]() ,
,![]() ,求证
,求证![]() ;
;
(3)甲问乙:“我取的k是一个整数,画出它的图象后发现抛物线与x轴的一个交点在y轴右侧,一个交点在原点和![]() 之间,你知道k等于几吗?并求出k的值.
之间,你知道k等于几吗?并求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更精准地关爱留守学生,某学校将留守学生的各种情形分成四种类型:A.由父母一方照看;B.由爷爷奶奶照看;C.由叔姨等近亲照看;D.直接寄宿学校.某数学小组随机调查了一个班级,发现该班留守学生数量占全班总人数的20%,并将调查结果制成如下两幅不完整的统计图.
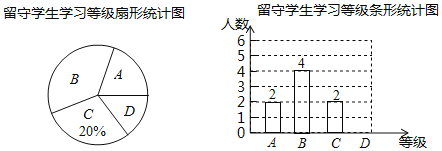
(1)该班共有 名留守学生,B类型留守学生所在扇形的圆心角的度数为 ;
(2)将条形统计图补充完整;
(3)已知该校共有2400名学生,现学校打算对D类型的留守学生进行手拉手关爱活动,请你估计该校将有多少名留守学生在此关爱活动中受益?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,已知∠ACB=90°,∠A=30°,BC=6,D为斜边AB上一点,以CD、CB为边作平行四边形CDEB,当AD=_____时,平行四边形CDEB为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,抛物线y=x2+3x﹣a2+a+2(a>1)的图象交x轴于点A和点B(点A在点B左侧),与y轴交于点C,顶点为E.
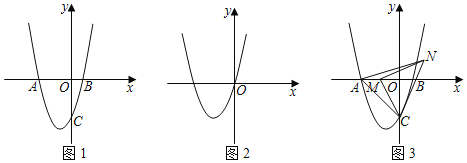
(1)如图1,求线段AB的长度(用含a的式子表示)及抛物线的对称轴;
(2)如图2,当抛物线的图象经过原点时,在平面内是否存在一点P,使得以A、B、E、P为顶点的四边形能否成为平行四边形?如果能,求出P点坐标;如果不能,请说明理由;
(3)如图3,当a=3时,若M点为x轴上一动点,连结MC,将线段MC绕点M逆时针旋转90°得到线段MN,连结AC、CN、AN,则△ACN周长的最小值为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2![]() ,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.

(1)求经过点O,C,A三点的抛物线的解析式.
(2)若点M是抛物线上一点,且位于线段OC的上方,连接MO、MC,问:点M位于何处时三角形MOC的面积最大?并求出三角形MOC的最大面积.
(3)抛物线上是否存在一点P,使∠OAP=∠BOC?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长度为6千米的国道![]() 两侧有
两侧有![]() ,
,![]() 两个城镇,从城镇到公路分别有乡镇公路连接,连接点为
两个城镇,从城镇到公路分别有乡镇公路连接,连接点为![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之间的距离为2千米,
之间的距离为2千米,![]() 、
、![]() 之间的距离为1千米,
之间的距离为1千米,![]() 、
、![]() 之间的乡镇公路长度为2.3千米,
之间的乡镇公路长度为2.3千米,![]() 、
、![]() 之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道
之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道![]() 上修建一个物流基地
上修建一个物流基地![]() ,设
,设![]() 、
、![]() 之间的距离为
之间的距离为![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和为
两个城镇的距离之和为![]() 干米,以下是对函数
干米,以下是对函数![]() 随自变量
随自变量![]() 的变化规律进行的探究,请补充完整.
的变化规律进行的探究,请补充完整.
(1)通过取点、画图、测量,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
(2)如图2,建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
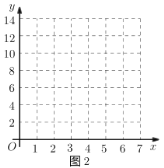
(3)结合画出的函数图象,解决问题:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和最小,则物流基地
两个城镇的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.
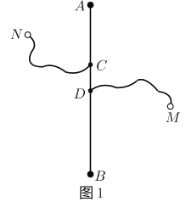
②如右图,有四个城镇![]() 、
、![]() 、
、![]() 、
、![]() 分别位于国道
分别位于国道![]() 两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地
两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距离之和最小,则物流基地
的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com