
 如图,点C、D在线段AB上,且△PCD是等边三角形.
如图,点C、D在线段AB上,且△PCD是等边三角形.分析 (1)根据等边三角形的性质得到∠PCD=∠PDC=60°,PC=CD=PD,根据外角的性质得到∠ACP=∠PDB=120°,然后根据相似三角形的判定即可得到结论;
(2)根据相似三角形的性质得到∠APC=∠PBD,根据外角的性质得到∠DPB+∠DBP=60°,于是得到结论.
解答 解:(1)当CD2=AC•DB时,△ACP∽△PDB,
∵△PCD是等边三角形,
∴∠PCD=∠PDC=60°,PC=CD=PD,
∴∠ACP=∠PDB=120°,
∵CD2=AC•DB,
∴$\frac{CD}{BD}=\frac{AC}{CD}$,即$\frac{PC}{BD}=\frac{AC}{PD}$,
∴△ACP∽△PDB;
(2)∵△ACP∽△PDB,
∴∠APC=∠PBD,
∵∠PDB=120°,
∴∠DPB+∠DBP=60°,
∴∠APC+∠BPD=60°,
∴∠APB=∠CPD+∠APC+∠BPD=120°.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图所示,现有两道互相垂直的墙,墙的东西方向长10米、南北方向长6米.张大爷想利用这两道墙围出一个面积为24平方米的矩形牛栏ABCD,牛栏的两边利用墙,另两边用长11米的篱笆围起来,问牛栏东西方向的长BC为多少米?
如图所示,现有两道互相垂直的墙,墙的东西方向长10米、南北方向长6米.张大爷想利用这两道墙围出一个面积为24平方米的矩形牛栏ABCD,牛栏的两边利用墙,另两边用长11米的篱笆围起来,问牛栏东西方向的长BC为多少米?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC,∠BAC=45°,BC=6,P是BC边上的一个三等分点,以点A为中心,把△ABP逆时针旋转45°,点P旋转到P′
如图,△ABC中,AB=AC,∠BAC=45°,BC=6,P是BC边上的一个三等分点,以点A为中心,把△ABP逆时针旋转45°,点P旋转到P′查看答案和解析>>
科目:初中数学 来源: 题型:解答题
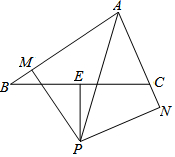 如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.
如图,在△ABC中,∠BAC的平分线与BC边的垂直平分线相交于点P,过点P作AB、AC(或延长线)的垂线,垂足分别是M、N,求证:BM=CN.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
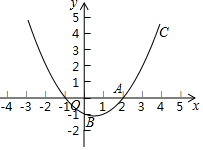 如图,已知二次函数y=ax2+bx+c的图象经过A(2,0),B(0,-1)和C(4,5)三点.
如图,已知二次函数y=ax2+bx+c的图象经过A(2,0),B(0,-1)和C(4,5)三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com