
 ��ͼ��һ�ű߳�Ϊ16cm��������ֽƬ�������ĸ����ϼ����ĸ��߳���ͬ��С�����ο������ǵij�������ӣ����������С�����εı߳�Ϊxcm�����ɵ��dz�������ӵ��ݻ�ΪVcm2��
��ͼ��һ�ű߳�Ϊ16cm��������ֽƬ�������ĸ����ϼ����ĸ��߳���ͬ��С�����ο������ǵij�������ӣ����������С�����εı߳�Ϊxcm�����ɵ��dz�������ӵ��ݻ�ΪVcm2��| x��cm�� | 1 | 2 | 3 | 4 | 5 |
| V��cm2�� |
| x��cm�� | 1 | 2 | 3 | 4 | 5 |
| V��cm2�� | 196 | 288 | 300 | 256 | 180 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 9 |
| 3 | 125 |
| 3 | -6 |
| 22 |
| 7 |
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��3��-9������ƽ���� |
| B��-3�ǣ�-3��2������ƽ���� |
| C��8���������ǡ�2 |
| D��16��ƽ�����ǡ�4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
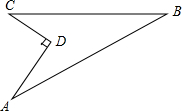 ��ͼ��ijסլС����ʩ��������������һ��յأ���֪AD=4�ף�CD=3�ף���ADC=90�㣬AB=13�ף�BC=12�ף�С��Ϊ�������������ڿյ����̲�ƺ����֪��ƺÿƽ����100Ԫ�������øò�ƺ�������յع��軨�Ѷ���Ԫ��
��ͼ��ijסլС����ʩ��������������һ��յأ���֪AD=4�ף�CD=3�ף���ADC=90�㣬AB=13�ף�BC=12�ף�С��Ϊ�������������ڿյ����̲�ƺ����֪��ƺÿƽ����100Ԫ�������øò�ƺ�������յع��軨�Ѷ���Ԫ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
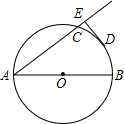 ��ͼ��AB��AC�ֱ��ǡ�O��ֱ�����ң�DΪ
��ͼ��AB��AC�ֱ��ǡ�O��ֱ�����ң�DΪ |
| BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
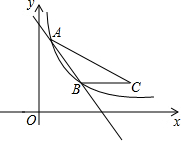 ��ͼ��ֱ��y=k1x+b�뷴��������y=
��ͼ��ֱ��y=k1x+b�뷴��������y=| k2 |
| x |
| k2 |
| x |
| m |
| x |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com