
°æƒø°øƒ≥–£◊È÷Ø—ß…˙ È∑®±»»¸£¨∂‘≤Œ»¸◊˜∆∑∞¥A°¢B°¢C°¢DÀƒ∏ˆµ»º∂Ω¯––¡À∆¿∂®£Æœ÷Àʪ˙≥È»°≤ø∑÷—ß…˙ È∑®◊˜∆∑µƒ∆¿∂®Ω·π˚Ω¯––∑÷Œˆ£¨≤¢ªÊ÷∆…»–ŒÕ≥º∆Õº∫ÕÃı–ŒÕ≥º∆Õº»Áœ¬£∫
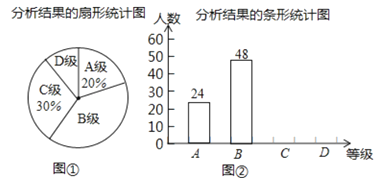
∏˘æð…œ ˆ–≈œ¢ÕÍ≥…œ¬¡–Œ £∫
£®1£©«Û’‚¥Œ≥È»°µƒ—˘±æµƒ»ð¡ø£ª
£®2£©«Î‘⁄Õº¢⁄÷–∞—Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®3£©“—÷™∏√–£’‚¥ŒªÓ∂Øπ≤ ’µΩ≤Œ»¸◊˜∆∑720∑𣨫΃„π¿º∆≤Œ»¸◊˜∆∑¥ÔµΩBº∂“‘…œ(º¥Aº∂∫ÕBº∂)”–∂ý…Ÿ∑ð£ø
°æ¥∞∏°ø£®1£©120£ª£®2£©œÍ«Èº˚Ω‚Œˆ£ª£®3£©432∑ð
°æΩ‚Œˆ°ø
£®1£©¿˚”√Aº∂µƒ»À ˝≥˝“‘∆‰À˘’ºµƒ∞Ÿ∑÷±»Ω¯“ª≤Ωº∆À„«Û≥ˆ¥∞∏º¥ø…£ª
£®2£©”√’‚¥Œµ˜≤ȵƒ◊лÀ ˝≥À“‘Cº∂À˘’ºµƒ∞Ÿ∑÷±»«Û≥ˆœý”¶µƒ»À ˝£¨»ª∫ÛΩ¯“ª≤Ω«Û≥ˆDº∂µƒ»À ˝£¨”…¥À≤π»´Ãı–ŒÕ≥º∆Õºº¥ø…£ª
£®3£©∏˘æð“‚£¨ ◊œ»«Û≥ˆBº∂“‘…œ’ºµƒ∞Ÿ∑÷±»£¨»ª∫ÛΩ¯“ª≤Ω≥À“‘720º¥ø….
£®1£©°þAº∂À˘’ºµƒ∞Ÿ∑÷±»Œ™![]() £¨∆‰»À ˝Œ™
£¨∆‰»À ˝Œ™![]() £¨
£¨
°ý’‚¥Œ≥È»°µƒ—˘±æ»ð¡øŒ™£∫![]() £¨
£¨
¥£∫’‚¥Œ≥È»°µƒ—˘±æµƒ»ð¡øŒ™120£ª
£®2£©∏˘æðCº∂À˘’ºµƒ∞Ÿ∑÷±»ø…µ√Cº∂»À ˝Œ™£∫![]() £®»À£©£¨
£®»À£©£¨
°ýDº∂»À ˝Œ™£∫![]() £®»À£©£¨
£®»À£©£¨
°ý≤π»´µƒÃı–ŒÕ≥º∆Õº»Áœ¬£∫
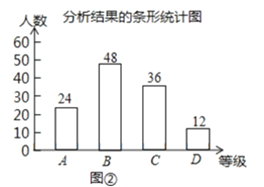
£®3£©°þBº∂“‘…œÀ˘’ºµƒ∞Ÿ∑÷±»Œ™£∫![]() £¨
£¨
°ý≤Œ»¸◊˜∆∑¥ÔµΩBº∂“‘…œµƒ∑ð ˝Œ™£∫![]() £®∑𣩣¨
£®∑𣩣¨
¥£∫≤Œ»¸◊˜∆∑¥ÔµΩBº∂“‘…œµƒ∑ð ˝Œ™432∑ð.



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–∫Ø ˝µƒÕºœÒ‘⁄√ø“ª∏ˆœÛœÞƒ⁄£¨ ![]() ÷µÀÊ
÷µÀÊ![]() ÷µµƒ‘ˆ¥Û∂¯‘ˆ¥Ûµƒ «£® £©
÷µµƒ‘ˆ¥Û∂¯‘ˆ¥Ûµƒ «£® £©
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº—º—œÚÃΩæø“ª‘™»˝¥Œ∑Ω≥Ãx3+2x2©Åx©Å2=0µƒΩ‚µƒ«Èøˆ£¨∏˘æð“‘Õ˘µƒ—ßœ∞æ≠—È£¨À˚œÎµΩ¡À∑Ω≥ÔÎ∫Ø ˝µƒπÿœµ£¨“ª¥Œ∫Ø ˝y=kx+b£®k°Ÿ0£©µƒÕºœÛ”Îx÷·Ωªµ„µƒ∫·◊¯±Íº¥Œ™“ª‘™“ª¥Œ∑Ω≥Ãkx+b£®k°Ÿ0£©µƒΩ‚£¨∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛ”Îx÷·Ωªµ„µƒ∫·◊¯±Íº¥Œ™“ª‘™∂˛¥Œ∑Ω≥Ãax2+bx+c=0£®a°Ÿ0£©µƒΩ‚£¨»Á£∫∂˛¥Œ∫Ø ˝y=x2©Å2x©Å3µƒÕºœÛ”Îx÷·µƒΩªµ„Œ™£®©Å1£¨0£©∫Õ£®3£¨0£©£¨Ωªµ„µƒ∫·◊¯±Í©Å1∫Õ3º¥Œ™x2©Å2x©Å3=0µƒΩ‚£Æ
∏˘æð“‘…œ∑Ω≥ÔÎ∫Ø ˝µƒπÿœµ£¨»Áπ˚Œ“√«÷±µΩ∫Ø ˝y=x3+2x2©Åx©Å2µƒÕºœÛ”Îx÷·Ωªµ„µƒ∫·◊¯±Í£¨º¥ø…÷™∑Ω≥Ãx3+2x2©Åx©Å2=0µƒΩ‚£Æ
º—º—Œ™¡ÀΩ‚∫Ø ˝y=x3+2x2©Åx©Å2µƒÕºœÛ£¨Õ®π˝√˵„∑®ª≠≥ˆ∫Ø ˝µƒÕºœÛ£Æ
x | °≠ | ©Å3 | ©Å | ©Å2 | ©Å | ©Å1 | ©Å | 0 |
| 1 |
| 2 | °≠ |
y | °≠ | ©Å8 | ©Å | 0 |
| m | ©Å | ©Å2 | ©Å | 0 |
| 12 | °≠ |
£®1£©÷±Ω”–¥≥ˆmµƒ÷µ£¨≤¢ª≠≥ˆ∫Ø ˝ÕºœÛ£ª
£®2£©∏˘æð±Ì∏Ò∫ÕÕºœÛø…÷™£¨∑Ω≥õƒΩ‚”–°° °°∏ˆ£¨∑÷±Œ™°° °°£ª
£®3£©ΩË÷˙∫Ø ˝µƒÕºœÛ£¨÷±Ω”–¥≥ˆ≤ªµ» Ωx3+2x2£æx+2µƒΩ‚ºØ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
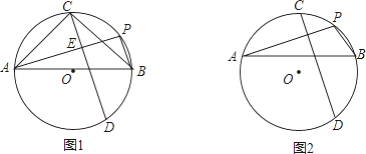
°æƒø°ø£®1£©»ÁÕº1£¨PA°¢PB «°—Oµƒ¡ΩÃıœ“£¨ABŒ™÷±æ∂£¨CŒ™![]() µƒ÷–µ„£¨œ“CD°ÕPA”⁄µ„E£¨–¥≥ˆAB”ÎACµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£ª
µƒ÷–µ„£¨œ“CD°ÕPA”⁄µ„E£¨–¥≥ˆAB”ÎACµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£ª
£®2£©»ÁÕº2£¨PA°¢PB «°—Oµƒ¡ΩÃıœ“£¨ABŒ™œ“£¨CŒ™¡”ª°![]() µƒ÷–µ„£¨œ“CD°ÕPA”⁄E£¨–¥≥ˆAE°¢PE”ÎPBµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£Æ
µƒ÷–µ„£¨œ“CD°ÕPA”⁄E£¨–¥≥ˆAE°¢PE”ÎPBµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
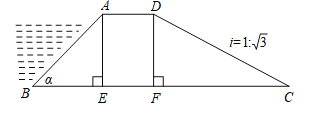
°æƒø°ø»ÁÕºÀ˘ 棨ƒ≥¿πÀÆ¥Û∞”µƒ∫·∂œ√ÊŒ™Ãð–ŒABCD£¨AE°¢DFŒ™Ã𖌵ƒ∏þ£¨∆‰÷–”≠ÀÆ∆¬ABµƒ∆¬Ω«¶¡=45°„£¨∆¬≥§AB=![]() √◊£¨±≥ÀÆ∆¬CDµƒ∆¬∂»i=1£∫
√◊£¨±≥ÀÆ∆¬CDµƒ∆¬∂»i=1£∫![]() £®iŒ™DF”ÎFCµƒ±»÷µ£©£¨‘Ú±≥ÀÆ∆¬CDµƒ∆¬≥§Œ™______√◊£Æ
£®iŒ™DF”ÎFCµƒ±»÷µ£©£¨‘Ú±≥ÀÆ∆¬CDµƒ∆¬≥§Œ™______√◊£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™πÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ãx2©Åx+m=0”–¡Ω∏ˆ≤ªœýµ»µƒ µ ˝∏˘£Æ
£®1£©«Û µ ˝mµƒ»°÷µ∑∂Œß£ª
£®2£©»Ù∑Ω≥õƒ¡Ω∏ˆ µ ˝∏˘Œ™x1°¢x2£¨«“x1+x2+x1x2=m2©Å1£¨«Û µ ˝mµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øº◊°¢““¡Ω»ÀΩ¯––”√´«Ú±»»¸£¨”√´«Ú∑…––µƒ¬∑œþŒ™≈◊ŒÔœþµƒ“ª≤ø∑÷£¨»ÁÕº£¨º◊‘⁄![]() µ„…œ’˝∑Ω
µ„…œ’˝∑Ω![]() µƒ
µƒ![]() ¥¶∑¢≥ˆ“ª«Ú£¨”√´«Ú∑…––µƒ∏þ∂»
¥¶∑¢≥ˆ“ª«Ú£¨”√´«Ú∑…––µƒ∏þ∂»![]() ”ÎÀÆ∆Ωæý¿Î
”ÎÀÆ∆Ωæý¿Î![]() ÷ƺ‰¬˙◊„∫Ø ˝±Ì¥Ô Ω
÷ƺ‰¬˙◊„∫Ø ˝±Ì¥Ô Ω![]() £Æ“—÷™µ„
£Æ“—÷™µ„![]() ”ΫÚÕ¯µƒÀÆ∆Ωæý¿ÎŒ™
”ΫÚÕ¯µƒÀÆ∆Ωæý¿ÎŒ™![]() £¨«ÚÕ¯µƒ∏þ∂»Œ™
£¨«ÚÕ¯µƒ∏þ∂»Œ™![]() £Æ
£Æ
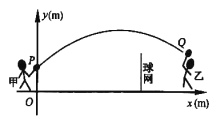
£®1£©µ±![]() ±£¨¢Ÿ«Û
±£¨¢Ÿ«Û![]() µƒ÷µ£Æ¢⁄Õ®π˝º∆À„≈–∂œ¥À«ÚƒÐ∑Òπ˝Õ¯£Æ
µƒ÷µ£Æ¢⁄Õ®π˝º∆À„≈–∂œ¥À«ÚƒÐ∑Òπ˝Õ¯£Æ
£®2£©»Ùº◊∑¢«Úπ˝Õ¯∫Û£¨”√´«Ú∑…––µΩµ„![]() µƒÀÆ∆Ωæý¿ÎŒ™
µƒÀÆ∆Ωæý¿ÎŒ™![]() £¨¿Îµÿ√ʵƒ∏þ∂»Œ™
£¨¿Îµÿ√ʵƒ∏þ∂»Œ™![]() µƒ
µƒ![]() ¥¶ ±£¨““ø€«Ú≥…𶣨«Û
¥¶ ±£¨““ø€«Ú≥…𶣨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®1£©“—÷™£∫»ÁÕº1£¨°˜ABC÷–£¨∑÷±“‘AB°¢ACŒ™“ª±þœÚ°˜ABCÕ‚◊˜’˝∑Ω–ŒABGE∫ÕACHF£¨÷±œþAN°ÕBC”⁄N£¨»ÙEP°ÕAN”⁄P£¨FQ°ÕAN”⁄Q£Æ≈–∂œœþ∂ŒEP°¢FQµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£ª
£®2£©»ÁÕº2£¨Ãð–ŒABCD÷–£¨AD°ŒBC£¨∑÷±“‘¡Ω—¸AB°¢CDŒ™“ª±þœÚÃð–ŒABCDÕ‚◊˜’˝∑Ω–ŒABGE∫ÕDCHF£¨œþ∂ŒADµƒ¥π÷±∆Ω∑÷œþΩªœþ∂ŒAD”⁄µ„M£¨ΩªBC”⁄µ„N£¨»ÙEP°ÕMN”⁄P£¨FQ°ÕMN”⁄Q£Æ£®1£©÷–Ω·¬€ªπ≥…¡¢¬£ø«ÎÀµ√˜¿Ì”…£Æ
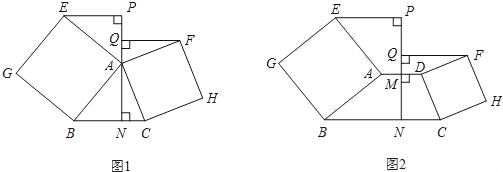
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄“ª∏ˆ≤ªÕ∏√˜µƒø⁄¥¸÷–◊∞”–3∏ˆ¥¯∫≈¬Îµƒ«Ú£¨«Ú∫≈∑÷±Œ™2£¨3£¨4£¨’‚–©«Ú≥˝∫≈¬Î≤ªÕ¨Õ‚∆‰À¸æ˘œýÕ¨°£º◊°¢““°¢¡ΩÕ¨—ßÕÊ√˛«Ú”Œœ∑£¨”Œœ∑πÊ‘Ú»Áœ¬£∫
œ»”…º◊Õ¨—ߥ”÷–Àʪ˙√˛≥ˆ“ª«Ú£¨º«œ¬«Ú∫≈£¨≤¢∑≈ªÿΩ¡‘»£¨‘Ÿ”…““Õ¨—ߥ”÷–Àʪ˙√˛≥ˆ“ª«Ú£¨º«œ¬«Ú∫≈°£Ω´º◊Õ¨—ß√˛≥ˆµƒ«Ú∫≈◊˜Œ™“ª∏ˆ¡ΩŒª ˝µƒ ÆŒª…œµƒ ˝£¨““Õ¨—ßµƒ◊˜Œ™∏ˆŒª…œµƒ ˝°£»Ù∏√¡ΩŒª ˝ƒÐ±ª4’˚≥˝£¨‘Úº◊ §£¨∑Ò‘Ú““ §.
Œ £∫’‚∏ˆ”Œœ∑π´∆Ω¬£ø«ÎÀµ√˜¿Ì”…°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com