Question

7．如图所示，在平面直角坐标系xOy中，Rt△AOB的直角边OB，OA分别在x轴上和y轴上，其中OA=2，OB=4，现将Rt△AOB绕着直角顶点O按逆时针方向旋转90°得到△COD，已知一抛物线经过C、D、B三点．
（1）该抛物线的解析式为y=-$\frac{1}{2}{x}^{2}$+x+4；
（2）设点E是抛物线上位于第一象限的动点，过点E作EF⊥x轴于点F，并交直线AB于N，过点E再作EM⊥AB于点M，求△EMN周长的最大值；
（3）当△EMN的周长最大时，在直线EF上是否存在点Q，使得△QCD是以CD为直角边的直角三角形？若存在请求出点Q的坐标，若不存在，请说明理由．

Answer 1

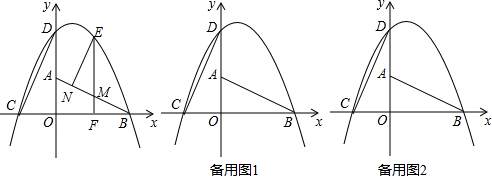
分析 （1）设抛物线的解析式为y=ax²+bx+c．由线段OA、OB的长度可得出点A、B的坐标，再由旋转的特性可得出点C、D的坐标，由点B、C、D三点的坐标利用待定系数法即可求出抛物线的解析式；
（2）在Rt△AOB中，找出∠ABO的正弦余弦值，再根据相似三角形的判定定理找出△EMN∽△BFN，从而得出∠MEN=∠FBN，用EN的长度来表示出EM和MN的长度，由点A、B的坐标利用待定系数法求出直线AB的函数解析式，设出点E的坐标为（t，-$\frac{1}{2}{t}^{2}$+t+4）（0＜t＜4），即可找出点N的坐标为（t，-$\frac{1}{2}$t+2），从而得出线段EN的长度，将EN、MN、EM相加即可得出△EMN的周长，根据二次函数的性质可求出EN的最大值，由此即可得出结论；
（3）结合（2）的结论可知直线EF的解析式为x=$\frac{3}{2}$，分∠QDC=90°和∠DCQ=90°两种情况来考虑，利用相似三角形的性质找出相似边的比例关系来找出线段的长度，再根据点与点间的数量关系即可找出点Q的坐标．

解答 解：（1）设抛物线的解析式为y=ax²+bx+c．
∵OA=2，OB=4，
∴点A（0，2），点B（4，0），
由旋转的特性可知：
点C（-2，0），点D（0，4）．
将点B（4，0）、点C（-2，0）、点D（0，4）代入到抛物线解析式得：
$\left\{\begin{array}{l}{0=16a+4b+c}\\{0=4a-2b+c}\\{4=c}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=1}\\{c=4}\end{array}\right.$．
∴该抛物线的解析式为y=-$\frac{1}{2}{x}^{2}$+x+4．
故答案为：y=-$\frac{1}{2}{x}^{2}$+x+4．
（2）依照题意画出图形，如图1所示．

在Rt△AOB中，OA=2，OB=4，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$，
∴sin∠ABO=$\frac{OA}{AB}=\frac{2}{2\sqrt{5}}=\frac{\sqrt{5}}{5}$，cos∠ABO=$\frac{OB}{AB}=\frac{4}{2\sqrt{5}}=\frac{2\sqrt{5}}{5}$．
∵EM⊥AB，EF⊥OB，
∴∠EMN=∠BFN=90°．
∵∠BNF=∠ENM，
∴△EMN∽△BFN，
∴∠MEN=∠FBN．
在Rt△EMN中，sin∠MEN=$\frac{MN}{EN}$，cos∠MEN=$\frac{EM}{EN}$，
∴MN=EN•sin∠MEN=EN•sin∠ABO=$\frac{\sqrt{5}}{5}$EN，
EM=EN•cos∠MEN=EN•cos∠ABO=$\frac{2\sqrt{5}}{5}$EN．
∴C_△EMN=EM+MN+EN=$\frac{2\sqrt{5}}{5}$EN+$\frac{\sqrt{5}}{5}$EN+EN=$\frac{5+3\sqrt{5}}{5}$EN．
由（1）知A（0，2）、B（4，0），设直线AB的解析式为：y=kx+2，
∴4k+2=0，解得：k=-$\frac{1}{2}$，
∴直线AB的解析式为：y=-$\frac{1}{2}$x+2．
设抛物线上点E的坐标为（t，-$\frac{1}{2}{t}^{2}$+t+4）（0＜t＜4），
∵EF⊥OB，
∴令y=-$\frac{1}{2}$x+2中x=t，y=-$\frac{1}{2}$t+2，
∴点N的坐标为（t，-$\frac{1}{2}$t+2），
∴EN=-$\frac{1}{2}{t}^{2}$+t+4-（-$\frac{1}{2}$t+2）=-$\frac{1}{2}{t}^{2}$+$\frac{3}{2}$t+2．
∴C_△EMN=$\frac{5+3\sqrt{5}}{5}$（-$\frac{1}{2}{t}^{2}$+$\frac{3}{2}$t+2）=-$\frac{5+3\sqrt{5}}{10}{t}^{2}$+$\frac{15+9\sqrt{5}}{10}$t+$\frac{10+6\sqrt{5}}{5}$（0＜t＜4）．
∴当t=-$\frac{b}{2a}$=$\frac{3}{2}$时，EN最大，此时C_△EMN最大，
∴C_△EMN最大为：$\frac{5+3\sqrt{5}}{5}$[-$\frac{1}{2}×（\frac{3}{2}）^{2}+\frac{3}{2}×\frac{3}{2}$+2]=$\frac{25+15\sqrt{5}}{8}$．
（3）由（2）知，当C_△EMN取最大值时，EF的解析式为：x=$\frac{3}{2}$．
①若∠QDC=90°，过点Q作QG⊥y轴于点G，如图2所示．

∵EF的解析式为：x=$\frac{3}{2}$，
∴QG=$\frac{3}{2}$，
∵∠QDG+∠DQG=90°，∠CDO+∠QDG=90°，
∴∠DGQ=∠CDO，
又∵∠QGD=∠DOC=90°，
∴△QDG∽△DCO，
∴$\frac{DG}{OC}=\frac{QG}{OD}$，
∴DG=2×$\frac{\frac{3}{2}}{4}$=$\frac{3}{4}$．
∴OG=OD-DG=4-$\frac{3}{4}$=$\frac{13}{4}$，
∴点Q的坐标为（$\frac{3}{2}$，$\frac{13}{4}$）；
②若∠DCQ=90°，如图3所示．

CF=$\frac{3}{2}$-（-2）=$\frac{7}{2}$，
∵∠QCF+∠OCD=90°，∠CDO+∠OCD=90°，
∴∠QCF=∠CDO，
又∵∠CFQ=∠DOC=90°，
∴△COD∽△QFC，
∴$\frac{FQ}{OC}=\frac{CF}{DO}$，即$\frac{FQ}{2}=\frac{\frac{7}{2}}{4}$，
∴FQ=$\frac{7}{4}$，
∴点Q的坐标为（$\frac{3}{2}$，-$\frac{7}{4}$）．
综上所述，当点Q的坐标为（$\frac{3}{2}$，$\frac{13}{4}$）或（$\frac{3}{2}$，-$\frac{7}{4}$）时，使得△QCD是以CD为直角边的直角三角形．

点评 本题考查了二次函数的性质、待定系数法求函数解析式、相似三角形的判定及性质以及三角形的周长，解题的关键是：（1）求出点B、C、D的坐标；（2）用线段EN的长度来表示△EMN的周长；（3）分两种情况考虑．本题属于中档题，难道不大，但非常繁琐，解决该题型题目时，依据题意作出图形，利用数形结合来解决问题是关键．