
【题目】如图,⊙O是△ABC的内切圆.
(1)若∠A=60°,连接BO、CO并延长,分别交AC、AB于点D、E,
① 求∠BOC的度数;
② 试探究BE、CD、BC之间的等量关系,并证明你的结论;
(2)若AB=AC=10,sin∠ABC=![]() ,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.
,AC、AB与⊙O相切于点D、E,将BC向上平移与⊙O交于点F、G,若以D、E、F、G为顶点的四边形是矩形,求平移的距离.

【答案】(1)①120°,②BC= BE+CD;(2)平移的距离是1.2.
【解析】分析:(1)①由点O是内心得∠BOC=120°;
②由切线长定理可证得.
(2),连接AO并延长,交BC于点N,交ED于点M,由以D、E、F、G为顶点的四边形是矩形,求得EF=3.6,再证明△AOE∽△ABN,求得![]() ,再证明△AED∽△ABC,得ED=3.2,即可求解.
,再证明△AED∽△ABC,得ED=3.2,即可求解.
详解:(1)①∵∠A=60°
∴∠ABC+∠ACB=120°
∵⊙O是△ABC的内切圆
∴ BD平分∠ABC,CE平分∠ACB
∴∠DBC+∠ECB=60°
∴∠BOC=120°
②BC= BE+CD
作∠BOC的平分线OF交BC于点F,
∵∠BOC=120°
∴∠BOE=60°,∠BOF=60°
在△BOE与 △BOF中


∴ △BOE≌△BOF(ASA)
∴ BE=BF
同理可证:CD=CF
∴ BC= BE+CD
(2)如图,连接AO并延长,交BC于点N,交ED于点M
∵⊙O是△ABC的内切圆
∴ AO是∠BAC的平分线,
又 AB=AC,
∴ AN⊥BC
∵AB=AC=10,sin∠ABC=![]()
∴ AN=8,BN=6
由切线长定理得:BN=BE=6,AE=AD=4,
∵点D、E是⊙O的切点,连接OE,∠AEO=∠ANB,∠BAN=∠BAN,

∴△AOE∽△ABN,![]() ,即
,即![]()
解得![]()
∴ ![]()
∵![]() ,∠BAC=∠BAC
,∠BAC=∠BAC
∴△AED∽△ABC
∴ ![]() ,
,![]()
以D、E、F、G为顶点的四边形是矩形
∴∠DEF=90°
∴ ![]() 是⊙O 的直径
是⊙O 的直径
∴ ![]()
∴平移的距离是![]()


科目:初中数学 来源: 题型:
【题目】已知一次函数y=kx+b的图象过P(1,4),Q(4,2)两点,且与x轴交于A点.
(1)求A点坐标;
(2)已知点M在x轴上,若使MP+MQ的值最小,求点M的坐标及MP+MQ的最小值;
(3)在(2)的条件下,在坐标平面内是否还存在一点N,使M,N,A,Q四点恰好构成平行四边形,若存在请求出点N的坐标,若不存在请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)解方程:3x+5=x+2请按所给导语,填写完整.
解:移项,得3x____=2____,(依据:_____).
合并同类项,得______,
系数化为1,得_____,(依据:______).
(2)解方程:2(x+15)=18﹣3(x﹣9).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面的5个时钟显示了同一时刻国外四个城市时间和北京时间,右图给出了国外四个城市与北京的时差,则下图中的时钟对应的城市依次是_____________________.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车往返于甲、乙两地之间,如果汽车以50千米/时的平均速度从甲地出发,则6小时可到达乙地.
(1)写出时间t(时)关于速度v(千米/时)的函数关系式,并画出函数图象.
(2)若这辆汽车需在5小时内从甲地到乙地,则此时汽车的平均速度至少应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)证明:“三角形内角和是180°”;
(2)请写出“直角三角形斜边上的中线等于斜边的一半”的逆命题,判断这一逆命题是真命题还是假命题,如果是真命题给出证明,如果是假命题,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售甲、乙两种运动鞋,2018年这两种鞋共卖出11000双。2019年甲种运动鞋卖出的数量比2018年增加6%,乙种运动鞋卖出的数量比2018年减少5%,且这两种鞋的总销量增加了2%.
(1)求2018年甲、乙两种运动鞋各卖了多少双?
(2)某制鞋厂组织工人生产甲、乙两种运动鞋。原计划安排 ![]() 的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
的工人生产甲种运动鞋,现抽调其中的16人去生产乙种运动鞋,已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双,若调配后制成的两种运动鞋数量相等,求该鞋厂工人的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
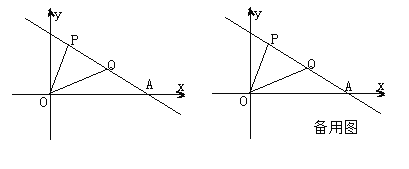
【题目】如图,O是直线![]() 上一点,
上一点,![]() 是一条射线,
是一条射线,![]() 平分
平分![]() ,
,![]() 在
在![]() 内,
内,![]() .
.
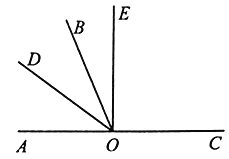
(1)若![]() ,垂足为O点,则
,垂足为O点,则![]() 的度数为________°,
的度数为________°,![]() 的度数为________°;在图中,与
的度数为________°;在图中,与![]() 相等的角有_________;
相等的角有_________;
(2)若![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B、C是正方形网格中的三个格点.
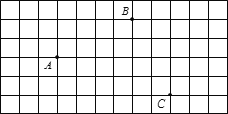
(1)①画射线AC;
②画线段BC;
③过点B画AC的平行线BD;
④在射线AC上取一点E,画线段BE,使其长度表示点B到AC的距离;
(2)在(1)所画图中,
①BD与BE的位置关系为 ;
②线段BE与BC的大小关系为BE BC(填“>”、“<”或“=”),理由是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com