
 的图象在第一限内的一个分支,点P是这条曲线的任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和F.
的图象在第一限内的一个分支,点P是这条曲线的任意一点,它的坐标是(a,b),由点P向x轴、y轴所作的垂线PM、PN(点M、N为垂足)分别与直线AB相交于点E和F.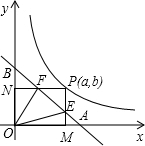 持不变的角?若有,请求出其大小;若没有,请说明理由.
持不变的角?若有,请求出其大小;若没有,请说明理由.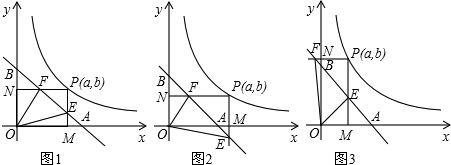
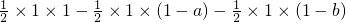
 ,
, ×1×b+
×1×b+ ×1×(a-1)=
×1×(a-1)= ,
,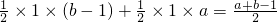 ,
, ;
;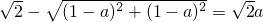 ,
,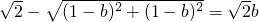 ,
,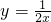 图象上任意一点,
图象上任意一点,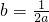 ,即2ab=1,
,即2ab=1, a×
a× b=1即,AF•BE=OB•OA,
b=1即,AF•BE=OB•OA,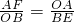 ,
,

 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:
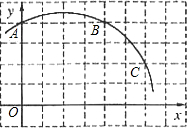 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.查看答案和解析>>
科目:初中数学 来源: 题型:
 12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )
12、如图,已知直角坐标系中的点A、B的坐标分别为A(2,4)、B(4,0),且P为AB的中点.若将线段AB向右平移3个单位后,与点P对应的点为Q,则点Q的坐标是( )查看答案和解析>>
科目:初中数学 来源: 题型:
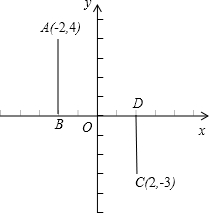 如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:
如图,已知直角坐标系中四点A(-2,4),B(-2,0),C(2,-3),D(2,0)、设P是x轴上的点,且PA、PB、AB所围成的三角形与PC、PD、CD所围成的三角形相似,请写出所有符合上述条件的点P的坐标:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com