
���� ��1��������������г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ����Խ���⣻
��2��������������г���Ӧ��һԪһ�β���ʽ�飬�Ӷ���������м��ֹ��������ַ���������ͣ�
��� �⣺��1����ÿ̨����x��Ԫ��ÿ̨���Ӱװ�y��Ԫ��
$\left\{\begin{array}{l}{x+2y=3.5}\\{2x+y=2.5}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=0.5}\\{y=1.5}\end{array}\right.$��
��ÿ̨����0.5��Ԫ��ÿ̨���Ӱװ�1.5��Ԫ��
��2�����蹺������ą�������Ӱװ壨30-a��̨��
$\left\{\begin{array}{l}{0.5a+1.5��30-a����28}\\{0.5a+1.5��30-a����30}\end{array}\right.$��
��ã�15��a��17��
��a=15��16��17��
�ʹ������ַ�����
����һ����������15̨�����Ӱװ�15̨���ܷ���Ϊ0.5��15+1.5��15=30��Ԫ��
����������������16̨�����Ӱװ�14̨���ܷ���Ϊ0.5��16+1.6��14=29��Ԫ��
����������������17̨�����Ӱװ�13̨���ܷ���Ϊ0.5��17+1.5��13=28��Ԫ��
�����������ͣ�
���� ���⿼��һԪһ�β���ʽ���Ӧ�á���Ԫһ�η������Ӧ�ã�����������Ĺؼ�����ȷ���⣬�г���Ӧ�ķ�����Ͳ���ʽ�飮


 ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д� С�����ϵ�д�
С�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=-20x+36 | B�� | y=-20x-4 | C�� | y=-20x+17 | D�� | y=-20x+15 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3$\sqrt{3}$ | B�� | 6 | C�� | 3 | D�� | $\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
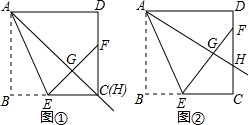
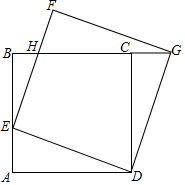 ��ͼ��������ABCD�ı߳�Ϊ2������E�ӵ�A�������ر�AB-BC���յ�C�˶�����DEΪ����������DEFG����D��E��F��G��˳ʱ�뷽�����У������E�˶����ٶ�Ϊÿ��1����λ���˶���ʱ��Ϊx �룮
��ͼ��������ABCD�ı߳�Ϊ2������E�ӵ�A�������ر�AB-BC���յ�C�˶�����DEΪ����������DEFG����D��E��F��G��˳ʱ�뷽�����У������E�˶����ٶ�Ϊÿ��1����λ���˶���ʱ��Ϊx �룮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������




�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com