练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    函数y＝的函数的定义域是

    [　　]

    A．x≥3

    B．x＞3

    C．x≥3且x≠4

    D．x≠3

    答案：C
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（带解析） 题型：解答题

    阅读下面的材料：
    在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y＝k1x＋b1（k1≠0）的图象为直线l1，一次函数y＝k2x＋b2（k2≠0）的图象为直线l2，若k1＝k2，且b1≠b2，我们就称直线l1与直线l2互相平行.

    解答下面的问题：
    （1）求过点P（1，4）且与已知直线y＝－2x－1平行的直线的函数表达式，并画出直线l的图象；
    （2）设直线l分别与y轴、x轴交于点A、B，如果直线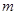：y＝kx＋t ( t＞0)与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式.

    查看答案和解析>>

    科目：初中数学 来源：2013届江苏省无锡市宜兴实验学校九年级5月中考适应性考试数学试卷（带解析） 题型：单选题

    定义[a，b，c]为函数y=ax2+bx+c的特征数，下面给出特征数为 [m，1-m，-1]的函数的一些结论：
    ① 当m＝-1时，函数图象的顶点坐标是（1，0）；
    ② 当m>0时，函数图象截x轴所得的线段长度大于1；
    ③ 当m<0时，函数在x>时，y随x的增大而减小；
    ④ 不论m取何值，函数图象经过一个定点．
    其中正确的结论有            （ ）

    A．4个B．3个C．2个D．1个

    查看答案和解析>>

    科目：初中数学 来源：2013-2014学年甘肃省九年级上学期期末考试数学试卷（解析版） 题型：填空题

    （定义[a,b,c]为函数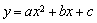的特征数,下面给出特征数为? [2m,1－m,－1－m]的函数的一些结论：

    ①当m＝－3时,函数图象的顶点坐标是（,）;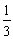

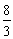    ②当m>0时,函数图象截x轴所得的线段长度大于;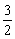

    ③当m<0时,函数在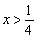时,y随x的增大而减小;

    ④当m≠0时,函数图象经过x轴上一个定点．

    其中正确的结论有________?????? ．（只需填写序号）

     

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年江苏省无锡市宜兴九年级5月中考适应性考试数学试卷（解析版） 题型：选择题

    定义[a，b，c]为函数y=ax2+bx+c的特征数，下面给出特征数为 [m，1-m，-1]的函数的一些结论：

    ① 当m＝-1时，函数图象的顶点坐标是（1，0）；

    ② 当m>0时，函数图象截x轴所得的线段长度大于1；

    ③ 当m<0时，函数在x>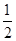时，y随x的增大而减小；

    ④ 不论m取何值，函数图象经过一个定点．

    其中正确的结论有            （ ）

    A．4个             B．3个              C．2个              D．1个

     

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年山东省济宁地区第一学期八年级期末考试数学试卷（解析版） 题型：解答题

    阅读下面的材料：

    在平面几何中，我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y＝k1x＋b1（k1≠0）的图象为直线l1，一次函数y＝k2x＋b2（k2≠0）的图象为直线l2，若k1＝k2，且b1≠b2，我们就称直线l1与直线l2互相平行.

    解答下面的问题：

    （1）求过点P（1，4）且与已知直线y＝－2x－1平行的直线的函数表达式，并画出直线l的图象；

    （2）设直线l分别与y轴、x轴交于点A、B，如果直线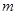：y＝kx＋t ( t＞0)与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式.

     

    查看答案和解析>>

    同步练习册答案