
【题目】在建设港珠澳大桥期间,大桥的规划选线须经过中华白海豚国家级白然保护区—区域![]() 或区域
或区域![]() .为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海
.为实现白海豚“零伤亡,不搬家”的目标,需合理安排施工时间和地点,为此,海豚观察员在相同条件下连续出海![]() 天,在区域
天,在区域![]() 、
、![]() 两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
两地对中华白海豚的踪迹进行了观测和统计,过程如下,请补充完整.(单位:头)
(收集数据)
连续![]() 天观察中华白海豚每天在区域
天观察中华白海豚每天在区域![]() 、区域
、区域![]() 出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
出现的数目情况,得到统计结果,并按从小到大的顺序排列如下:
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
区域 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(整理、描述数据)
(1)按如下数段整理、描述这两组数据,请补充完整:
海豚数 |
|
|
|
|
|
区域 |
|
|
| _________ | _________ |
区域 |
|
|
|
|
|
(2)两组数据的平均数、中位数,众数如下所示:
观测点 | 平均数 | 中位数 | 众数 |
区域 |
|
|
|
区域 |
|
|
|
请填空:上表中中位数![]() _______,,众数
_______,,众数![]() ______;
______;
(3)规划者们选择了区域![]() 为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的
为大桥的必经地,为减少施工对白海豚的影响,合理安排施工时间,估计在接下来的![]() 天施工期内,区域
天施工期内,区域![]() 大约有多少天中华白海豚出现的数目在
大约有多少天中华白海豚出现的数目在![]() 的范围内?
的范围内?
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)区域
;(3)区域![]() 大约有
大约有![]() 天中华白海豚出现的数目在
天中华白海豚出现的数目在![]() 的范围内.
的范围内.
【解析】
(1)统计观察的数据,可填写表格;
(2)先对区域A的数据从小到大排列,找出最中间2个数值,取平均数为中位数,观察出现次数最多的数值为众数;
(3)用出现在A区域的比例×总天数可得.
(1)根据统计数据,得出:
22≤x<28的有2天,29≤x≤35的有1天
故填写:![]() ,
,![]() .
.
(2)统计A区域的数据,发现x=6的有3天,出现次数最多
∴众数为:6
统计数据已经从小到大排列,一共有20组数据,第10和第11组数据是最中间两,分别为:8、8
∴平均数为8,∴中位数为:8
故填写:![]() ,
,![]() .
.
(3)![]() (天),
(天),
答:区域![]() 大约有
大约有![]() 天中华白海豚出现的数目在22≤x≤35的范围内.
天中华白海豚出现的数目在22≤x≤35的范围内.


科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.
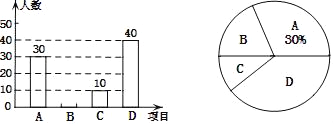
请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2与x轴交于两点A(﹣1,0)和B(4,0),与Y轴交于点C,连接AC、BC、AB,
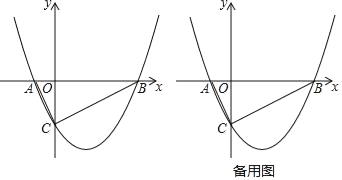
(1)求抛物线的解析式;
(2)点D是抛物线上一点,连接BD、CD,满足![]() ,求点D的坐标;
,求点D的坐标;
(3)点E在线段AB上(与A、B不重合),点F在线段BC上(与B、C不重合),是否存在以C、E、F为顶点的三角形与△ABC相似,若存在,请直接写出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC内接于⊙O,∠BAC的平分线交⊙O于点D,交BC于点E(BE>EC),且BD=2![]() .过点D作DF∥BC,交AB的延长线于点F.
.过点D作DF∥BC,交AB的延长线于点F.
(1)求证:DF为⊙O的切线;
(2)若∠BAC=60°,DE=![]() ,求图中阴影部分的面积;
,求图中阴影部分的面积;
(3)若![]() ,DF+BF=8,如图2,求BF的长.
,DF+BF=8,如图2,求BF的长.
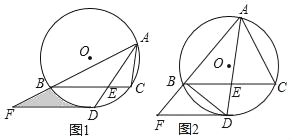
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个小球从斜坡的点O处抛出,小球的抛出路线可以用二次函数y=4x﹣![]() x2刻画,斜坡可以用一次函数y=
x2刻画,斜坡可以用一次函数y=![]() x刻画,下列结论错误的是( )
x刻画,下列结论错误的是( )

A. 当小球抛出高度达到7.5m时,小球水平距O点水平距离为3m
B. 小球距O点水平距离超过4米呈下降趋势
C. 小球落地点距O点水平距离为7米
D. 斜坡的坡度为1:2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为直径在矩形
为直径在矩形![]() 内作半圆
内作半圆![]() .
.
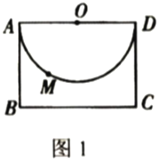
(1)若点![]() 是半圆
是半圆![]() 上一点,则点
上一点,则点![]() 到
到![]() 的最小距离为________;
的最小距离为________;
(2)如图2,保持矩形![]() 固定不动,将半圆
固定不动,将半圆![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]()
![]() 度,得到半圆
度,得到半圆![]() ,则当半圆
,则当半圆![]() 与
与![]() 相切时,求旋转角
相切时,求旋转角![]() 的度数;
的度数;

(3)在旋转过程中,当![]() 与边
与边![]() 有交点时,求
有交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
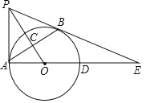
【题目】如图,PA与⊙O相切于点A,过点A作AB⊥OP,垂足为C,交⊙O于点B.连接PB,AO,并延长AO交⊙O于点D,与PB的延长线交于点E.
(1)求证:PB是⊙O的切线;
(2)若OC=3,AC=4,求PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,记函数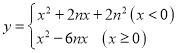 的图象为
的图象为![]() ,正方形
,正方形![]() 的对称中心与原点重合,顶点
的对称中心与原点重合,顶点![]() 的坐标为(2,2),点
的坐标为(2,2),点![]() 在第四象限.
在第四象限.
(1)当![]() =1时.
=1时.
①求![]() 的最低点的纵坐标;
的最低点的纵坐标;
②求图象![]() 上所有到
上所有到![]() 轴的距离为2的横坐标之和.
轴的距离为2的横坐标之和.
③若当![]() ≤
≤![]() ≤
≤![]() 时,-9≤
时,-9≤![]() ≤2,则
≤2,则![]() 、
、![]() 的对应值为 .
的对应值为 .
(2)当图象![]() 与正方形
与正方形![]() 的边恰好有两个公共点时,直接写出
的边恰好有两个公共点时,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com