
【题目】如图,已知点A(1,2)是反比例函数y= ![]() 图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 .
图象上的一点,连接AO并延长交双曲线的另一分支于点B,点P是x轴上一动点;若△PAB是等腰三角形,则点P的坐标是 . 
【答案】(﹣3,0)或(5,0)或(3,0)或(﹣5,0)
【解析】解:∵反比例函数y= ![]() 图象关于原点对称, ∴A、B两点关于O对称,
图象关于原点对称, ∴A、B两点关于O对称,
∴O为AB的中点,且B(﹣1,﹣2),
∴当△PAB为等腰三角形时有PA=AB或PB=AB,
设P点坐标为(x,0),
∵A(1,2),B(﹣1,﹣2),
∴AB= ![]() =2
=2 ![]() ,PA=
,PA= ![]() ,PB=
,PB= ![]() ,
,
当PA=AB时,则有 ![]() =2
=2 ![]() ,解得x=﹣3或5,此时P点坐标为(﹣3,0)或(5,0);
,解得x=﹣3或5,此时P点坐标为(﹣3,0)或(5,0);
当PB=AB时,则有 ![]() =2
=2 ![]() ,解得x=3或﹣5,此时P点坐标为(3,0)或(﹣5,0);
,解得x=3或﹣5,此时P点坐标为(3,0)或(﹣5,0);
综上可知P点的坐标为(﹣3,0)或(5,0)或(3,0)或(﹣5,0),
故答案为:(﹣3,0)或(5,0)或(3,0)或(﹣5,0).
由对称性可知O为AB的中点,则当△PAB为等腰三角形时只能有PA=AB或PB=AB,设P点坐标为(x,0),可分别表示出PA和PB,从而可得到关与x的方程,可求得x,可求得P点坐标.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y= ![]() x与双曲线y=
x与双曲线y= ![]() 的交点A的横坐标为2
的交点A的横坐标为2
(1)求k的值
(2)如图,过点P(m,3)(m>0)作x轴的垂线交双曲线y= ![]() (x>0)于点M,交直线OA于点N
(x>0)于点M,交直线OA于点N 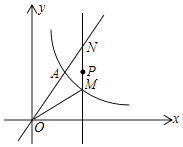
①连接OM,当OA=OM时,直接写出PN﹣PM的值
②试比较PM与PN的大小,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
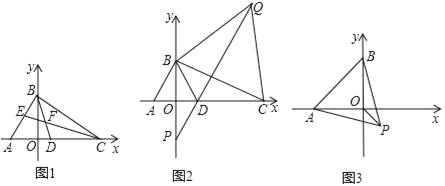
【题目】如图,在平面直角坐标系中,A(﹣3,0),点 B是 y轴正半轴上一动点,点C、D在 x正半轴上.
(1)如图,若∠BAO=60°,∠BCO=40°,BD、CE 是△ABC的两条角平分线,且BD、CE交于点F,直接写出CF的长_____.
(2)如图,△ABD是等边三角形,以线段BC为边在第一象限内作等边△BCQ,连接 QD并延长,交 y轴于点 P,当点 C运动到什么位置时,满足 PD=![]() DC?请求出点C的坐标;
DC?请求出点C的坐标;
(3)如图,以AB为边在AB的下方作等边△ABP,点B在 y轴上运动时,求OP的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备购进一批节能灯,已知1只A型节能灯和3只B型节能灯共需26元;3只A型节能灯和2只B型节能灯共需29元.
(1)求一只A型节能灯和一只B型节能灯的售价各是多少元;
(2)学校准备购进这两种型号的节能灯共50只,并且A型节能灯的数量不多于B型节能灯数量的3倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)填空:与∠AOE互补的角有 ;
(2)若∠COD=30°,求∠DOE的度数;
(3)当∠AOD=α°时,请直接写出∠DOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.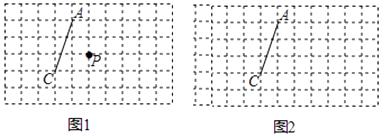
(1)如图1,点P在小正方形的顶点上,在图1中作出点P关于直线AC的对称点Q,连接AQ、QC、CP、PA,并直接写出四边形AQCP的周长;
(2)在图2中画出一个以线段AC为一条对角线、面积为15的菱形ABCD,且点B和点D均在小正方形的顶点上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com