
【题目】我们提供如下定理:在直角三角形中,30°的锐角所对的直角边是斜边的一半,
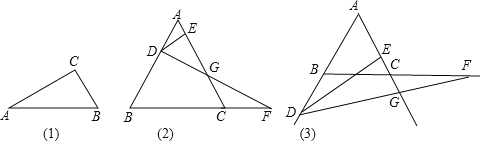
如图(1),Rt△ABC中,∠C=90°,∠A=30°,则BC=![]() AB.
AB.
请利用以上定理及有关知识,解决下列问题:
如图(2),边长为6的等边三角形ABC中,点D从A出发,沿射线AB方向有A向B运动点F同时从C出发,以相同的速度沿着射线BC方向运动,过点D作DE⊥AC,DF交射线AC于点G.
(1)当点D运动到AB的中点时,直接写出AE的长;
(2)当DF⊥AB时,求AD的长及△BDF的面积;
(3)小明通过测量发现,当点D在线段AB上时,EG的长始终等于AC的一半,他想当点D运动到图3的情况时,EG的长始终等于AC的一半吗?若改变,说明理由;若不变,说明理由.
【答案】(1)AE =![]() ;(2)AD=2,S△BDF=8
;(2)AD=2,S△BDF=8![]() ;(3)不变,理由见解析
;(3)不变,理由见解析
【解析】
(1)根据D为AB的中点,求出AD的长,在Rt△ADE中,利用30°所对的直角边等于斜边的一半求出AE的长即可;
(2)根据题意得到设AD=CF=x,表示出BD与BF,在Rt△BDF中,利用30°所对的直角边等于斜边的一半得到BF=2BD,列出关于x的方程,求出方程的解得到x的值,确定出BD与BF的长,利用勾股定理求出DF的长,即可确定出△BDF的面积;
(3)不变,理由如下,如图,过F作FM⊥AG延长线于M,由AD=CF,且△ABC为等边三角形,利用等边三角形的性质及锐角三角函数定义得到DE=FM,以及AE=CM,利用AAS得到△DEG与△FMC全等,利用全等三角形对应边相等得到EG=MG,根据AC=AE+EC,等量代换即可得证.
解:(1)当D为AB中点时,AD=BD=![]() AB=3,
AB=3,
在Rt△ADE中,∠A=60°,
∴∠ADE=30°,
∴AE=![]() AD=
AD=![]() ;
;
(2)设AD=x,∴CF=x,
则BD=6-x,BF=6+x,
∵∠B=60°,∠BDF=90°,
∴∠F=30°,即BF=2BD,
∴6+x=2×(6-x),
解得:x=2,即AD=2,
∴BD=4,BF=8,
根据勾股定理得:DF=![]() 4
4![]() ,
,
∴S△BDF=![]() ×4×4
×4×4![]() =8
=8![]() ;
;
(3)不变,理由如下,如图,过F作FM⊥AG延长线于M,
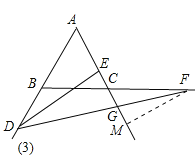
∵△ABC为等边三角形,
∴∠A=∠ACB=∠FCM=60°,
在Rt△ADE和Rt△FCM中,
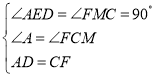
∴Rt△ADE≌Rt△FCM,
∴DE=FM,AE=CM,
在△DEG和△FMG,
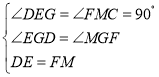 ,
,
∴△DEG≌△FMG,
∴GE=GM,
∴AC=AE+EC=CM+CE=GE+GM=2GE.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
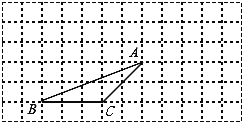
【题目】如图,△ABC的顶点都在方格纸的格点上,将△ABC向右平移4格,再向上平移2格,其中每个格子的边长为1个单位长度。
⑴在图中画出平移后的△A′B′C′;
⑵若连接AA′、CC′,则这两条线段的关系是 ;
⑶作△ABC的高AD,并求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在平面直角坐标系中,点
,在平面直角坐标系中,点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,将线段
,将线段![]() 先向上平移
先向上平移![]() 个单位长度,再向右平移
个单位长度,再向右平移![]() 个单位长度,得到线段
个单位长度,得到线段![]() ,连接
,连接![]() ,
,![]() ,构成平行四边形
,构成平行四边形![]() .
.
(1)请写出点![]() 的坐标为________,点
的坐标为________,点![]() 的坐标为________,
的坐标为________,![]() ________;
________;
(2)点![]() 在
在![]() 轴上,且
轴上,且![]() ,求出点
,求出点![]() 的坐标;
的坐标;
(3)如图![]() ,点
,点![]() 是线段
是线段![]() 上任意一个点(不与
上任意一个点(不与![]() 、
、![]() 重合),连接
重合),连接![]() 、
、![]() ,试探索
,试探索![]() 、
、![]() 、
、![]() 之间的关系,并证明你的结论.
之间的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中,且A![]() 、B
、B![]() 、C
、C![]() .将其平移后得到
.将其平移后得到![]() ,若A,B的对应点是
,若A,B的对应点是![]() ,
,![]() ,C的对应点
,C的对应点![]() 的坐标是
的坐标是![]() .
.
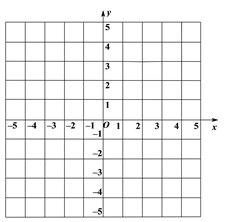
(1)在平面直角坐标系中画出△ABC;
(2)写出点![]() 的坐标是_____________,
的坐标是_____________,![]() 坐标是___________;
坐标是___________;
(3)此次平移也可看作![]() 向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
向________平移了____________个单位长度,再向_______平移了______个单位长度得到△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
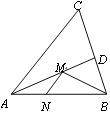
【题目】如图,在锐角△ABC中,AB=4,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB是某天然气公司的主输气管道,点C、D是在AB异侧的两个小区,现在主输气管道上寻找支管道连接点,向两个小区铺设管道![]() 有以下两个方案:
有以下两个方案:
方案一:只取一个连接点P,使得像两个小区铺设的支管道总长度最短,在图中标出点P的位置,保留画图痕迹;
方案二:取两个连接点M和N,使得点M到C小区铺设的支管道最短,使得点N到D小区铺设的管道最![]() 短在途中标出M、N的位置,保留画图痕迹;
短在途中标出M、N的位置,保留画图痕迹;

设方案一中铺设的支管道总长度为L1![]() ,方案二中铺设的支管道总长度为
,方案二中铺设的支管道总长度为![]() ,则L1与L2的大小关系为: L1_____ L2(填
,则L1与L2的大小关系为: L1_____ L2(填![]() ”、
”、![]() ”或)理由是______.
”或)理由是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=36°,∠C=72°,点D在AC上,BC=BD,DE∥BC交AB于点E,则图中等腰三角形共有( )

A. 3个B. 4个C. 5个D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”“=”),当∠A=40°时,∠B+∠C+∠1+∠2=______.
(3)如图③,是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=360°-(∠B+∠C+∠1+∠2)=360°- = ,猜想∠BDA+∠CEA与∠A的关系为

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com