
 如图,在边长为1个单位长度的小正方形组成的网格中.
如图,在边长为1个单位长度的小正方形组成的网格中.分析 (1)根据图形平移的性质画出△A′B′C′即可;
(2)根据△ABC内的格点数可得出L的值,同理得出L的值,利用正方形的面积减去三个顶点上三角形的面积即可得出S的值;
(3)求出ab的值,再把N=12,L=8代入进行计算即可.
解答 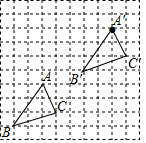 解:(1)如图△A?B?C?即为所求;
解:(1)如图△A?B?C?即为所求;
(2)由图可知N=3,L=3,S=3×3-$\frac{1}{2}$×3×1-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×3=3.5.
故答案为:3,3,3.5;
(3)∵由题意得$\left\{\begin{array}{l}{3+3a+b=3.5}\\{1+6a+b=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-1}\end{array}\right.$
∴S=N+$\frac{1}{2}$L-1
∴当N=12,L=8时,S=15.
点评 本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
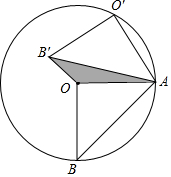 如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.
如图,在Rt△AOB中,∠AOB=Rt∠,OA=OB=2,将△AOB绕点A按顺时针旋转至△AO′B′,使点O′落在以O为圆心,OA长为半径的圆上,则△AOB′的面积是$\sqrt{3}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 两数之和必大于任何一个加数 | |
| B. | 同号两数相加,符号不变,并把绝对值相加 | |
| C. | 两负数相加和为负数,并把绝对值相减 | |
| D. | 异号两数相加,取绝对值较大的加数的符号,并把绝对值相加 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com