练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．先化简，再求值：[4x（x-y）-（2x-y）2]÷（-2y），其中x=$\frac{1}{2}$，y=-2．

    分析 根据整式的混合运算顺序和运算法则化简原式，再代入求值可得．

    解答 解：原式=[4x2-4xy-（4x2-4xy+y2）]÷（-2y）
    =（4x2-4xy-4x2+4xy-y2）÷（-2y）
    =（-y2）÷（-2y）
    =$\frac{1}{2}$y，
    当y=-2时，原式=-1．

    点评 本题主要考查整式的化简求值，熟练掌握整式的混合运算顺序和运算法则是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．若a，b，c都是非零有理数，试讨论 $\frac{a}{|a|}$+$\frac{b}{|b|}$+$\frac{c}{|c|}$+$\frac{abc}{{|{abc}|}}$所有可能的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．已知实数x，y满足$\sqrt{x-2}$+（y+1）2=0，求x-y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．流花河的警戒水位是33.5米，表记录的是今年某一周内的水位变化情况，取河流的警戒水位作为0点，并且上周末（星期六）的水位达到警戒水位，（正号表示水位比前一天上升，负号表示水位比前一天下降．）
    星期日一二三四五六
    水位变化
    （米）    		+0.3+0.81-0.32+0.04+0.27-0.35-0.02
    （1）本周哪一天河流的水位最高？哪一天河流的水位最低？
    （2）与上周末相比，本周末河流的水位是上升了还是下降了？
    （3）以警戒水位作为零点，用折线统计图表示本周的水位情况．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．收入25元表示+25元，则支出20元应表示为-20元．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    7．下列各数中的无理数是（　　）
    A．$\root{3}{9}$B．0.9C．$\sqrt{9}$D．$\frac{1}{9}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．我们知道：$\frac{1}{1}$-$\frac{1}{2}$=$\frac{1}{1×2}$，$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{2×3}$，┅┅
    那么反过来也成立．如：$\frac{1}{1×2}$=$\frac{1}{1}$-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$┅┅
    则计算：①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+┅┅+$\frac{1}{98×99}$+$\frac{1}{99×100}$
    ②$\frac{2}{1×3}$+$\frac{2}{3×5}$+$\frac{2}{5×7}$+$\frac{2}{7×9}$+┅┅+$\frac{2}{97×99}$+$\frac{2}{99×101}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．若m+n=7，mn=12，则m2+n2的值是（　　）
    A．1B．25C．2D．-10

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

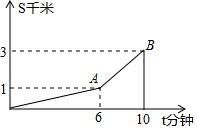    12．小强骑车从家到学校要经过一段先上坡后下坡的路，在这段路上小强骑车的距离s（千米）与骑车的时间t（分钟）之间的函数关系如图所示，请根据图中信息回答下列问题：
    （1）小强去学校时下坡路长2千米；
    （2）小强下坡的速度为0.5千米/分钟；
    （3）若小强回家时按原路返回，且上坡的速度不变，下坡的速度也不变，那么回家骑车走这段路的时间是14分钟．

    查看答案和解析>>

    同步练习册答案