
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上的一个动点(不与点A重合),延长ME交CD的延长线于点N,连接MD,AN. 
(1)求证:四边形AMDN是平行四边形.
(2)当AM的值为何值时,四边形AMDN是矩形?请说明理由.
【答案】
(1)证明:∵四边形ABCD是菱形,
∴ND∥AM,
∴∠NDE=∠MAE,∠DNE=∠AME,
∵点E是AD中点,
∴DE=AE,
在△NDE和△MAE中,
 ,
,
∴△NDE≌△MAE(AAS),
∴ND=MA,
∴四边形AMDN是平行四边形
(2)AM=1.
理由如下:∵四边形ABCD是菱形,
∴AD=AB=2,
∵平行四边形AMDN是矩形,
∴DM⊥AB,
即∠DMA=90°,
∵∠DAB=60°,
∴∠ADM=30°,
∴AM= ![]() AD=1
AD=1
【解析】(1)根据菱形的性质可得ND∥AM,再根据两直线平行,内错角相等可得∠NDE=∠MAE,∠DNE=∠AME,根据中点的定义求出DE=AE,然后利用“角角边”证明△NDE和△MAE全等,根据全等三角形对应边相等得到ND=MA,然后利用一组对边平行且相等的四边形是平行四边形证明;(2)根据矩形的性质得到DM⊥AB,再求出∠ADM=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半解答.


科目:初中数学 来源: 题型:
【题目】图1为长方形纸片ABCD,AD=26,AB=22,直线L、M皆为长方形的对称轴.今将长方形纸片沿着L对折后,再沿着M对折,并将对折后的纸片左上角剪下直角三角形,形成一个五边形EFGHI,如图2.最后将图2的五边形展开后形成一个八边形,如图2,且八边形的每一边长恰好均相等.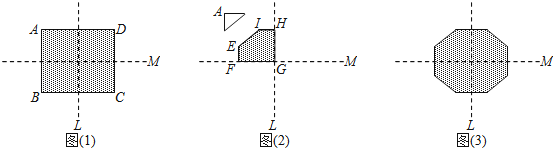
(1)若图2中HI长度为x,请以x分别表示剪下的直角三角形的勾长和股长.
(2)请求出图3中八边形的一边长的数值,并写出完整的解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图,△MNP中,∠P=60°,MN=NP,MQ⊥PN,垂足为Q,延长MN至G,取NG=NQ,若△MNP的周长为12,MQ=a,则△MGQ周长是( )
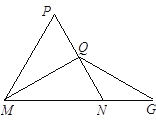
A. 8+2a B. 8+a C. 6+a D. 6+2a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是( ) 
A.a>0
B.3是方程ax2+bx+c=0的一个根
C.a+b+c=0
D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A,B两点,抛物线y=x2+bx+c经过A,B两点,点C是抛物线与x轴的另一个交点(与A点不重合).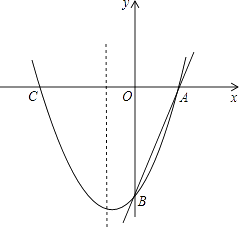
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D为△ABC内一点,且BD=AD.
(1)求证:CD⊥AB;
(2)∠CAD=15°,E为AD延长线上的一点,且CE=CA.
①求证:DE平分∠BDC;
②若点M在DE上,且DC=DM,请判断ME、BD的数量关系,并给出证明;
③若N为直线AE上一点,且△CEN为等腰三角形,直接写出∠CNE的度数.
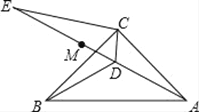
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com