
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )
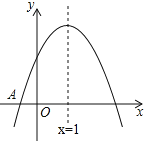
A.①③④B.①②③C.①②④D.①②③④
【答案】B
【解析】
①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),当x>3时,y<0,故①正确;
②抛物线开口向下,故a<0,∵![]() ,∴2a+b=0.∴3a+b=0+a=a<0,故②正确;
,∴2a+b=0.∴3a+b=0+a=a<0,故②正确;
③设抛物线的解析式为y=a(x+1)(x﹣3),则![]() ,令x=0得:y=﹣3a.∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴
,令x=0得:y=﹣3a.∵抛物线与y轴的交点B在(0,2)和(0,3)之间,∴![]() .解得:
.解得:![]() ,故③正确;
,故③正确;
④.∵抛物线y轴的交点B在(0,2)和(0,3)之间,∴2≤c≤3,由![]() 得:
得:![]() ,∵a<0,∴
,∵a<0,∴![]() ,∴c﹣2<0,∴c<2,与2≤c≤3矛盾,故④错误.
,∴c﹣2<0,∴c<2,与2≤c≤3矛盾,故④错误.
解:①由抛物线的对称性可求得抛物线与x轴令一个交点的坐标为(3,0),
当x>3时,y<0,
故①正确;
②抛物线开口向下,故a<0,
∵![]() ,
,
∴2a+b=0.
∴3a+b=0+a=a<0,
故②正确;
③设抛物线的解析式为y=a(x+1)(x﹣3),则![]() ,
,
令x=0得:y=﹣3a.
∵抛物线与y轴的交点B在(0,2)和(0,3)之间,
∴![]() .
.
解得:![]() ,
,
故③正确;
④.∵抛物线y轴的交点B在(0,2)和(0,3)之间,
∴2≤c≤3,
由![]() 得:
得:![]() ,
,
∵a<0,
∴![]() ,
,
∴c﹣2<0,
∴c<2,与2≤c≤3矛盾,
故④错误.
故选B.


科目:初中数学 来源: 题型:
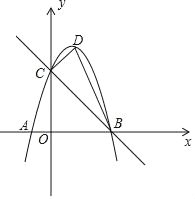
【题目】如图,以D为顶点的抛物线y=﹣x2+bx+c交x轴于A、B两点,交y轴于点C,直线BC的表达式为y=﹣x+3.
(1)求抛物线的表达式;
(2)在直线BC上有一点P,使PO+PA的值最小,求点P的坐标;
(3)在x轴上是否存在一点Q,使得以A、C、Q为顶点的三角形与△BCD相似?若存在,请求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察如图,填表后再回答问题:
(1)在横线上填入正确的数:
![]() 的个数:8,______ ,24
的个数:8,______ ,24![]()
★的个数:1,4,______ ![]()
(2)试求第6个图形中“![]() ”的个数和“
”的个数和“![]() ”的个数?
”的个数?
(3)试求第108个图形中“![]() ”的个数与“
”的个数与“![]() ”的个数之差?
”的个数之差?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班分别选5名同学参加“学雷锋读书活动”演讲比赛,其预赛成绩如图:

(1)根据上图求出下表所缺数据;
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8 | 10 | 1.6 |
(2)根据上表中的平均数、中位数和方差你认为哪班的成绩较好?并说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值 ;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB,
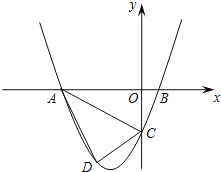
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
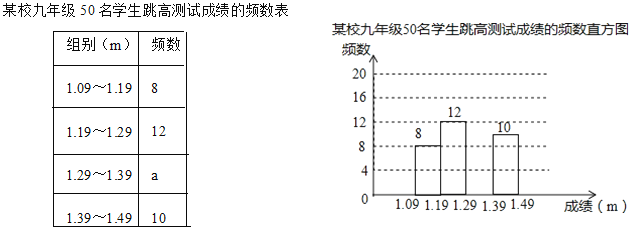
(1)求a的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售每台进价分别为200元,170元的A,B两种型号的电风扇,表中是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A,B两种型号的电风扇的销售单价.
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,则A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润为1400元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com