

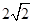 时(如图),求证:CD是⊙O的切线;
时(如图),求证:CD是⊙O的切线;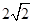 时,CD所在直线于⊙O相交,设另一交点为E,连接AE.
时,CD所在直线于⊙O相交,设另一交点为E,连接AE.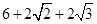 ②存在,这样的梯形有2个
②存在,这样的梯形有2个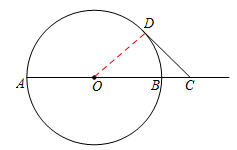
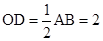 。
。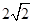 ,
, 。
。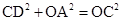 。
。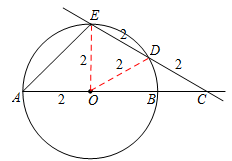
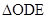 为等边三角形。
为等边三角形。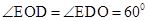 。
。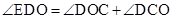 ,
,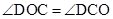 ,
,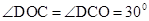 ,∴
,∴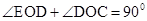 ,即
,即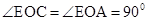 。
。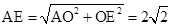 ,
,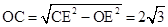 。
。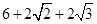 。
。
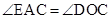 。
。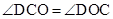 。
。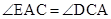 ,∴AE=CE。
,∴AE=CE。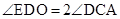 ,
,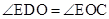 ,
,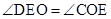 。
。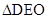 ∽
∽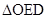 。
。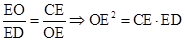 ,即:
,即: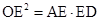 。
。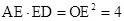 。
。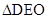 ∽
∽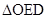 ,从而由比例式可求解。
,从而由比例式可求解。

 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
cm,轴截面上有两点P、Q,PA=40cm,BQ=30cm,则圆柱的侧面上P、Q两点的最短距离是 .
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 AB,C、D是半圆AB的两个三等分点,连接PD.
AB,C、D是半圆AB的两个三等分点,连接PD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com