
分析 (1)直接利用二次根式的乘除运算法则化简求出即可;
(2)首先化简二次根式进而合并同类二次根式即可.
解答 解:(1)$\sqrt{18}$÷$\sqrt{\frac{3}{4}}$×$\sqrt{\frac{4}{3}}$
=3$\sqrt{2}$×$\sqrt{\frac{4}{3}}$×$\sqrt{\frac{4}{3}}$
=3$\sqrt{2}$×$\frac{4}{3}$
=4$\sqrt{2}$;
(2)2$\sqrt{2}$-4$\sqrt{\frac{1}{27}}$+3$\sqrt{48}$
=2$\sqrt{2}$-4×$\frac{\sqrt{3}}{9}$+3×4$\sqrt{3}$
=2$\sqrt{2}$-$\frac{4\sqrt{3}}{9}$+12$\sqrt{3}$
=2$\sqrt{2}$+$\frac{104\sqrt{3}}{9}$.
点评 此题主要考查了二次根式的混合运算,正确化简二次根式是解题关键.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:解答题
| 商品 | 成本价(元/个) | 销售价(元/个) |
| 甲 | 20 | 40 |
| 乙 | 30 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
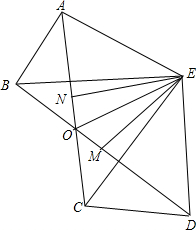 如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:
如图,BE=CE,AB=DC,∠ABE=∠DCE,连接AC、DB交于点O,连接OE,EM、EN分别平分∠AEC和∠BED.求证:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com