
【题目】已知![]() 四个点.
四个点.
(1)在图中描出![]() ,
,![]() ,
,![]() ,
,![]() 四个点,顺次连接
四个点,顺次连接![]() 四点;
四点;
(2)直接写出线段![]() 之间的位置关系_____________;
之间的位置关系_____________;
(3)求四边形![]() 的面积
的面积
(4)将四边形![]() 向右平移2个单位长度,向上平移4个单位长度得到四边形
向右平移2个单位长度,向上平移4个单位长度得到四边形![]() 写出各顶点坐标
写出各顶点坐标![]() ___________,
___________,![]() ____________,
____________,![]() ____________,
____________,![]() ____________.
____________.
【答案】(1)见解析;(2)AB∥CD且AB=CD;(3)15;(4)![]() 坐标为(-1,2),
坐标为(-1,2),![]() 坐标为(4,2),
坐标为(4,2),![]() 坐标为(5,5),
坐标为(5,5),![]() 坐标为(0,5).
坐标为(0,5).
【解析】
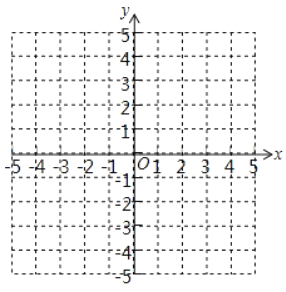
(1)根据A(-3,-2),B(2,-2),C(3,1),D(-2,1),在图中描出A,B,C,D四个点,并顺次连接点A,B,C,D,A即可.
(2)根据图示,写出线段AB,CD之间的位置关系和数量关系即可.
(3)根据平行四边形的面积=底×高,求出四边形ABCD的面积是多少即可.
(4)找到向右平移2个单位长度,向上平移4个单位长度后各点的对应点,可得出点各点的坐标.
解:(1)
 .
.
(2)AB,CD之间的关系是:
AB∥CD且AB=CD.
(3)[2-(-3)]×[1-(-2)]
=5×3
=15
答:四边形ABCD的面积是15.
(4)![]() 坐标为(-1,2),
坐标为(-1,2),![]() 坐标为(4,2),
坐标为(4,2),![]() 坐标为(5,5),
坐标为(5,5),![]() 坐标为(0,5).
坐标为(0,5).


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】好学小东同学,在学习多项式乘以多项式时发现:(![]() x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为:
x+4)(2x+5)(3x-6)的结果是一个多项式,并且最高次项为:![]() x2x3x=3x3,常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:
x2x3x=3x3,常数项为:4×5×(-6)=-120,那么一次项是多少呢?要解决这个问题,就是要确定该一次项的系数.根据尝试和总结他发现:一次项系数就是:![]() ×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x.
×5×(-6)+2×(-6)×4+3×4×5=-3,即一次项为-3x.
请你认真领会小东同学解决问题的思路,方法,仔细分析上面等式的结构特征.结合自己对多项式乘法法则的理解,解决以下问题.
(1)计算(x+2)(3x+1)(5x-3)所得多项式的一次项系数为_____.
(2)(![]() x+6)(2x+3)(5x-4)所得多项式的二次项系数为_______.
x+6)(2x+3)(5x-4)所得多项式的二次项系数为_______.
(3)若计算(x2+x+1)(x2-3x+a)(2x-1)所得多项式不含一次项,求a的值;
(4)若(x+1)2021=a0x2021+a1x2020+a2x2019+···+a2020x+a2021,则a2020=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数y=x2+mx+2的图象经过点A,B,顶点为D.
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1 , 顶点为D1 . 点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了调查某小区居民的用水情况,随机抽查了10户家庭的月用水量,结果如下表:
月用水量(吨) | 4 | 5 | 6 | 9 |
户数 | 3 | 4 | 2 | 1 |
则关于这10户家庭的月用水量,下列说法错误的是 ( )
A.中位数是5吨
B.众数是5吨
C.极差是3吨
D.平均数是5.3吨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,分别根据下列条件,写出各点的坐标.
(1)若点![]() 在
在![]() 轴上,位于原点上方,距离原点2个单位长度,则点
轴上,位于原点上方,距离原点2个单位长度,则点![]() __________;
__________;
(2)若点![]() 在
在![]() 轴上,位于原点右侧,距离原点1个单位长度,则点
轴上,位于原点右侧,距离原点1个单位长度,则点![]() __________;
__________;
(3)若点![]() 在
在![]() 轴上方,
轴上方,![]() 轴右侧,距离每条坐标轴都是2个单位长度,则点
轴右侧,距离每条坐标轴都是2个单位长度,则点![]() __________;
__________;
(4)若点![]() 在
在![]() 轴上,位于原点右侧,距离原点3个单位长度,则点
轴上,位于原点右侧,距离原点3个单位长度,则点![]() _________.
_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
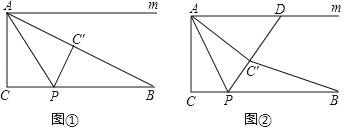
【题目】已知∠ACB=90°,AC=2,CB=4.点P为线段CB上一动点,连接AP,△APC与△APC′关于直线AP对称,其中点C的对称点为点C′.直线m过点A且平行于CB
(1)如图①:连接AB,当点C落在线段AB上时,求BC′的长;
(2)如图②:当PC=![]() BC时,延长PC′交直线m于点D,求△ADC′面积;
BC时,延长PC′交直线m于点D,求△ADC′面积;
(3)在(2)的条件下,连接BC′,直接写出线段BC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
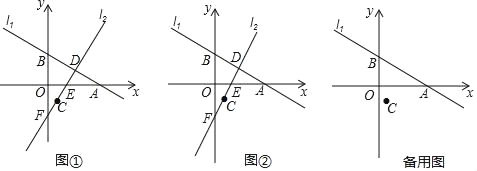
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+2![]() 与x轴、y轴分别交于点A、B两点,OA=
与x轴、y轴分别交于点A、B两点,OA=![]() OB,直线l2:y=k2x+b经过点C(1,﹣
OB,直线l2:y=k2x+b经过点C(1,﹣![]() ),与x轴、y轴和线段AB分别交于点E、F、D三点.
),与x轴、y轴和线段AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
(2)如图①:若EC=ED,求点D的坐标和△BFD的面积;
(3)如图②:在坐标轴上是否存在点P,使△PCD是以CD为底边的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣3﹣(﹣4)+7;
(2)计算:![]() ;
;
(3)计算:![]() ;
;
(4)计算:﹣14﹣(﹣2)2+6×(﹣![]() );
);
(5)化简:3x2+5x﹣5x2+3x;
(6)化简:6(m2﹣n)﹣3(n+2m2).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,∠BAE+∠AED=180°,∠1=∠2,那么∠M=∠N(下面是推理过程,请你填空).
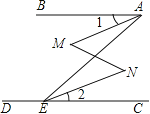
解:∵∠BAE+∠AED=180°(已知)
∴ ∥ (同旁内角互补,两直线平行)
∴∠BAE= (两直线平行,内错角相等)
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ (内错角相等,两直线平行)
∴∠M=∠N(两直线平行,内错角相等)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com