
【题目】某商场经销一种成本价为20元/件的商品,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于成本价的1.8倍,在试销售过程中发现每天的销量y(件)与售价x(元/件)之间满足一次函数关系,对应关系如下表所示:

(1)求y与x之间的函数表达式,并写出自变量x的取值范围;
(2)该商场销售这种商品每天所获得的利润为w元,若每天销售这种商品需支付人员工资、管理费等各项费用共200元,求w与x之间的函数表达式;并求出这种商品销售单价定为多少时,才能使商场每天获取的利润最大?最大利润是多少?
【答案】(1)![]() ;(2)
;(2)![]() ,销售单价定为36元/件时,利润最大,最大为888元
,销售单价定为36元/件时,利润最大,最大为888元
【解析】
(1)设y与x之间的函数表达式为y=kx+b,利用待定系数法求得函数解析式,再根据销售价不高于成本价的1.8倍,可得自变量x的取值范围;
(2)根据(售价﹣成本)×销售数量=销售利润,列出函数关系式,然后配方,写成顶点式,根据二次函数的性质及问题的实际意义,可得答案.
解:(1)设y与x之间的函数表达式为y=kx+b,根据题意得:![]() ,
,
解得:![]() ,
,
∴y=﹣2x+140,
又20×1.8=36,
∴自变量x的取值范围是20≤x≤36;
(2)w=(x﹣20)y﹣200
=(2﹣20)(﹣2x+140)﹣200
=﹣2x2+180x﹣3000
=﹣2(x﹣45)2+1050,
∵﹣2<0,
∴抛物线开口向下,当x<45时,w随x的增大而增大,
又20≤x≤36,
∴当x=36时,w取得最大值,最大值为:
﹣2(36﹣45)2+1050=﹣2×81+1050=888(元).
∴w与x之间的函数表达式为w=﹣2x2+180x﹣3000,这种商品销售单价定为36元/件时,才能使商场每天获取的利润最大,最大利润是888元.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,矩形OABC的顶点O是直角坐标系的原点,点A、C分别在x轴、y轴上,点B的坐标为(8,4),将矩形OABC绕点A顺时针旋转得到矩形ADEF,D、E、F分别与B、C、O对应,EF的延长线恰好经过点C,AF与BC相交于点Q.
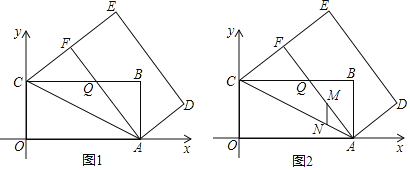
(1)证明:△ACQ是等腰三角形;
(2)求点D的坐标;
(3)如图2,动点M从点A出发在折线AFC上运动(不与A、C重合),经过的路程为x,过点M作AO的垂线交AC于点N,记线段MN在运动过程中扫过的面积为S;求S关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
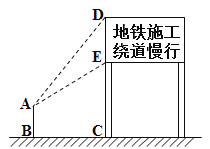
【题目】某市地铁工程正在加快建设,为了缓解市区内一些主要路段交通拥挤的现状,交警大队在一些主要路口设立了交通路况指示牌,如图所示,小明在离指示牌3.2米的点B处测得指示牌顶端D点和底端E点的仰角分别为52°和30°.求路况指示牌DE的高度.(精确到0.01米,参考数据:![]() ≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
≈1.732,sin52°≈0.79,cos52°≈0.62, tan52°≈1.28.)
查看答案和解析>>
科目:初中数学 来源: 题型:
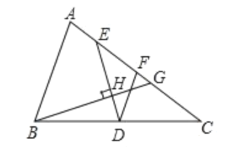
【题目】如图,在![]() 中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且
中,AB<AC,点D、F分别为BC、AC的中点,E点在边AC上,连接DE,过点B作DE的垂线交AC于点G,垂足为点H,且![]() 与四边形ABDE的周长相等,设AC=b,AB=c.
与四边形ABDE的周长相等,设AC=b,AB=c.
(1)求线段CE的长度;
(2)求证:DF=EF;
(3)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
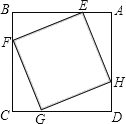
【题目】如图,正方形ABCD边长为4,E、F、G、H分别是AB、BC、CD、DA上的点,且AE=BF=CG=DH.设A、E两点间的距离为x,四边形EFGH的面积为y,则y与x的函数图象可能是( )
A.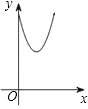 B.
B.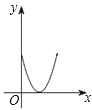
C.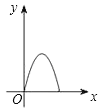 D.
D.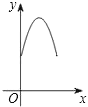
查看答案和解析>>
科目:初中数学 来源: 题型:
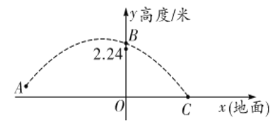
【题目】2019年女排世界杯于9月在日本举行,中国女排以十一连胜的骄人成绩卫冕冠军,充分展现了团队协作、顽强拼搏的女排精神.如图是某次比赛中垫球时的动作,若将垫球后排球的运动路线近似的看作拋物线,在同一竖直平面内建立如图所示的直角坐标系,已知运动员垫球时(图中点![]() )离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点
)离球网的水平距离为5米,排球与地面的垂直距离为0.5米,排球在球网上端0.26米处(图中点![]() )越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点
)越过球网(女子排球赛中球网上端距地面的高度为2.24米),落地时(图中点![]() )距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )
)距球网的水平距离为2.5米,则排球运动路线的函数表达式为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,![]() 和
和![]() 是两个全等的直角三角形纸片,其中
是两个全等的直角三角形纸片,其中![]() ,
,![]() ,
,![]() .
.
解决问题
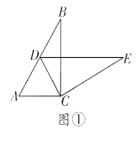
(1)如图①,智慧小组将![]() 绕点
绕点![]() 顺时针旋转,发现当点
顺时针旋转,发现当点![]() 恰好落在
恰好落在![]() 边上时,
边上时,![]() ,请你帮他们证明这个结论;
,请你帮他们证明这个结论;
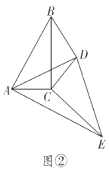
(2)缜密小组在智慧小组的基础上继续探究,连接![]() ,当
,当![]() C绕点
C绕点![]() 继续旋转到如图②所示的位置时,他们提出
继续旋转到如图②所示的位置时,他们提出![]() ,请你帮他们验证这一结论是否正确,并说明理由;
,请你帮他们验证这一结论是否正确,并说明理由;
探索发现
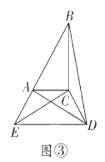
(3)如图③,勤奋小组在前两个小组的启发下,继续旋转![]() ,当
,当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(4)在图①的基础上,写出一个边长比为![]() 的三角形(可添加字母).
的三角形(可添加字母).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小颖“综合与实践”小组学习了三角函数后,开展了测量本校旗杆高度的实践活动.他们制订了测量方案,并利用课余时间完成了实地测量.他们在该旗杆底部所在的平地上,选取两个不同测点,分别测量了该旗杆顶端的仰角以及这两个测点之间的距离.为了减小测量误差,小组在测量仰角的度数以及两个测点之间的距离时,都分别测量了两次并取它们的平均值作为测量结果,如表是不完整测量数据.
课题 | 测量旗杆的高度 | |||
成员 | 组长:小颖,组员:小明,小刚,小英 | |||
测量工具 | 测量角度的仪器,皮尺等 | |||
测量示意图 |
| 说明: 线段GH表示学校旗杆,测量角度的仪器的高度AC=BD=1.62m,测点A,B与H在同一水平直线上,A,B之间的距离可以直接测得,且点G,H,A,B,C,D都在同一竖直平面内,点C,D,E在同一条直线上,点E在GH上. | ||
测量数据 | 测量项目 | 第一次 | 第二次 | 平均值 |
∠GCE的度数 | 30.6° | 31.4° | 31° | |
∠GDE的度数 | 36.8° | 37.2° | 37° | |
A,B之间的距离 | 10.1m | 10.5m | m | |
… | … | |||
(1)任务一:完成表格中两次测点A,B之间的距离的平均值.
(2)任务二:根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆GH的高度.(精确到0.1m)(参考数据:sin31°≈0.51,cos31°≈0.86,tan31°≈0.60,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河南省开封市铁塔始建于公元1049年(北宋皇祐元年),是国家重点保护文物之一,在900多年中,历经了数次地震、大风、水患而巍然屹立,素有“天下第一塔”之称.如图,小明在铁塔一侧的水平面上一个台阶的底部A处测得塔顶P的仰角为45°,走到台阶顶部B处,又测得塔顶P的仰角为38.7°,已知台阶的总高度BC为3米,总长度AC为10米,试求铁塔的高度.(结果精确到1米,参考数据:sin38.7°≈0.63,cos38.7°≈0.78,tan38.7°≈0.80)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com