
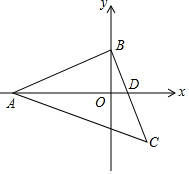
 如图,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),点C在第四象限,BC与x轴交于点D(q,0),x轴恰好平分∠BAC,则点C的坐标为( )
如图,在等腰Rt△ABC中,∠ABC=90°,A(p,0),B(0,r),点C在第四象限,BC与x轴交于点D(q,0),x轴恰好平分∠BAC,则点C的坐标为( )| A. | (r,$\frac{p-q}{2}$) | B. | (-$\frac{p}{2}$,$\frac{p-q}{2}$) | C. | (r,p+q) | D. | (2q,$\frac{p-r}{2}$) |
分析 如图,作CE⊥y轴于E,CM⊥x轴交AB的延长线于F.由△ABO≌△BCE,推出CE=OB=r,由△ABD≌△CBF,推出AD=CF=q-p,推出CM=$\frac{1}{2}$CF=$\frac{q-p}{2}$,由此即可解决问题.
解答 解:如图,作CE⊥y轴于E,CM⊥x轴交AB的延长线于F.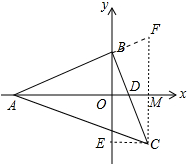
∵BA=BC,∠ABC=90°,
∴∠BAC=45°,
∵AD平分∠BAC,
∴∠BAO=∠CAO=22.5°,
∵∠AMF=∠AMC=90°,
∴∠F=∠ACF=∠ABO=67.5°,∠CBE=∠BAO=22.5°,
∴AF=AC,
∴FM=MC,
在△ABO和△BCE中,
$\left\{\begin{array}{l}{∠AOB=∠BEC}\\{∠BAO=∠CBE}\\{AB=BC}\end{array}\right.$,
∴△ABO≌△BCE,
∴CE=OB=r,
在△ABD和△CBF中,
$\left\{\begin{array}{l}{∠ABD=∠CBF}\\{∠ADB=∠F=67.5°}\\{AB=BC}\end{array}\right.$,
∴△ABD≌△CBF,
∴AD=CF=q-p,
∴CM=$\frac{1}{2}$CF=$\frac{q-p}{2}$,
∵点C在第四象限,
∴C(r,$\frac{P-q}{2}$),
故选A.
点评 本题考查等腰直角三角形的性质、全等三角形的判定和性质、坐标与图形的性质、角平分线的性质等知识,解题的关键是正确寻找全等三角形,学会添加常用辅助线,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{9}=±3$ | B. | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | C. | $\sqrt{{{(-3)}^2}}=-3$ | D. | ${(-\sqrt{3})^2}=3$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 1 | 2 | 3 | 4 | … |
| 2 | 4 | 6 | 8 | … |
| 3 | 6 | 9 | 12 | … |
| 4 | 8 | 12 | 16 | … |
| … | … | … | … | … |
| 20 | a |
| 24 | b |
| c | 35 |
| A. | 15,18,28 | B. | 22,27,25 | C. | 24,30,28 | D. | 25,30,28 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | $2\sqrt{5}$ | C. | $\frac{{18\sqrt{3}}}{13}$ | D. | $\frac{{12\sqrt{3}}}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 如果|$\overrightarrow{a}$|=|$\overrightarrow{b}$|,那么$\overrightarrow{a}$=$\overrightarrow{b}$ | B. | 如果|$\overrightarrow{a}$|=|-$\overrightarrow{b}$|,那么$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C. | 如果$\overrightarrow{a}$∥$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| | D. | 如果$\overrightarrow{a}$=-$\overrightarrow{b}$,那么|$\overrightarrow{a}$|=|$\overrightarrow{b}$| |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
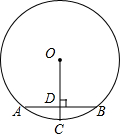 如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )
如图,AB为⊙O的弦,AB=6cm,OC⊥AB于D,交⊙O于点C,且CD=1cm,则⊙O的半径为( )| A. | 5cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/kg) | 售价(元/kg) | |
| 甲种 | 5 | 8 |
| 乙种 | 9 | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com