
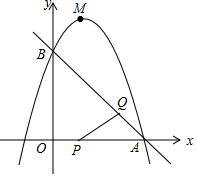
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线分析 (1)先利用直线解析式确定A点和B点坐标,然后利用待定系数法求抛物线的解析式;
(2)OP=t,AQ=$\sqrt{2}$t,则PA=3-t,先判断∠QAP=45°,讨论:当∠PQA=90°时,如图①,利用等腰直角三角形的性质得PA=$\sqrt{2}$AQ,即3-t=$\sqrt{2}$•$\sqrt{2}$t;当∠APQ=90°时,如图②,利用等腰直角三角形的性质得AQ=$\sqrt{2}$AP,即$\sqrt{2}$t=$\sqrt{2}$•(3-t),然后分别解关于t的方程即可;
(3)如图③,延长FQ交x轴于点H,设点P的坐标为(t,0),则点E的坐标为(t,-t+3),易得△AQH为等腰直角三角形,则AH=HQ=$\frac{\sqrt{2}}{2}$AQ=t,则可表示出点Q的坐标为(3-t,t),点F的坐标为[3-t,-(3-t)2+2(3-t)+3)],所以FQ=-t2+3t,再证明四边形PQFE为平行四边形得到EP=FQ.即3-t=3t-t2,然后解方程求出t即可得到点F的坐标;
(4)如图④所示:OP=t,AQ=$\sqrt{2}$t,则BQ=3$\sqrt{2}$-$\sqrt{2}$t,利用配方法得到y=-(x-1)2+4,则点M的坐标为(1,4),利用两点间的距离公式得到MB=$\sqrt{2}$,AB=3$\sqrt{2}$,AM=2$\sqrt{5}$,于是根据勾股定理的逆定理可证明∠ABM=90°,根据相似三角形的判断方法,由于∠QBM=∠BOP,则当$\frac{BM}{OP}$=$\frac{BQ}{OB}$时,△BOP∽△QBM时,即$\frac{\sqrt{2}}{t}$=$\frac{3\sqrt{2}-\sqrt{2}t}{3}$或当$\frac{BM}{OB}$=$\frac{BQ}{OP}$时,△BOP∽△MBQ,即$\frac{\sqrt{2}}{3}$=$\frac{3\sqrt{2}-\sqrt{2}t}{t}$,然后分别解关于t的方程即可.
解答 解:(1)当y=0时,-x+3=0,解得x=3,则A点坐标为(3,0),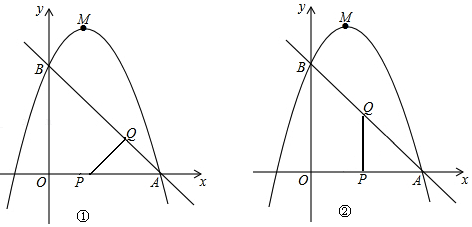
当x=0时,y=-x+3=3,则B点坐标为(0,3),
将A(3,0),B(0,3)代入y=-x2+bx+c得$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3;
(2)OP=t,AQ=$\sqrt{2}$t,则PA=3-t,
∵OA=OB=3,∠BOA=90°,
∴∠QAP=45°.
当∠PQA=90°时,如图①,PA=$\sqrt{2}$AQ,即3-t=$\sqrt{2}$•$\sqrt{2}$t,解得t=1;
当∠APQ=90°时,如图②,AQ=$\sqrt{2}$AP,即$\sqrt{2}$t=$\sqrt{2}$•(3-t),解得t=$\frac{3}{2}$;
综上所述,当t=1或t=$\frac{3}{2}$时,△PQA是直角三角形;
(3)如图③,延长FQ交x轴于点H,设点P的坐标为(t,0),则点E的坐标为(t,-t+3),
易得△AQH为等腰直角三角形,
∴AH=HQ=$\frac{\sqrt{2}}{2}$AQ=$\frac{\sqrt{2}}{2}$•$\sqrt{2}$t=t,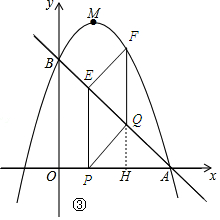
∴点Q的坐标为(3-t,t),点F的坐标为[3-t,-(3-t)2+2(3-t)+3)],
∴FQ=-(3-t)2+2(3-t)+3)-t=-t2+3t,
∵EP∥FQ,EF∥PQ,
∴四边形PQFE为平行四边形,
∴EP=FQ.即3-t=3t-t2,解得t1=1,t2=3(舍去),
∴点F的坐标为(2,3);
(4)存在.
如图④所示:OP=t,AQ=$\sqrt{2}$t,则BQ=3$\sqrt{2}$-$\sqrt{2}$t,
∵y=-x2+2x+3=-(x-1)2+4,
∴点M的坐标为(1,4),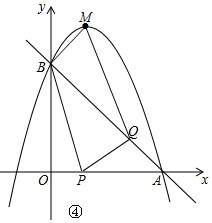
∴MB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
而AB=3$\sqrt{2}$,AM=$\sqrt{(1-3)^{2}+{4}^{2}}$=2$\sqrt{5}$,
∴AB2+BM2=AM2,
∴△ABM为直角三角形,∠ABM=90°,
∵∠QBM=∠BOP,
∴当$\frac{BM}{OP}$=$\frac{BQ}{OB}$时,△BOP∽△QBM时,即$\frac{\sqrt{2}}{t}$=$\frac{3\sqrt{2}-\sqrt{2}t}{3}$,
整理得t2-3t+3=0,△=32-4×1×3<0,方程无实数解:
当$\frac{BM}{OB}$=$\frac{BQ}{OP}$时,△BOP∽△MBQ,即$\frac{\sqrt{2}}{3}$=$\frac{3\sqrt{2}-\sqrt{2}t}{t}$,解得t=$\frac{9}{4}$,
综上所述,当t=$\frac{9}{4}$时,以B,Q,M为顶点的三角形与以O,B,P为顶点的三角形相似.
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角三角形的性质和平行四边形的判定与性质;会利用待定系数法求抛物线解析式;会利用勾股定理的逆定理判断直角三角形,灵活应用相似三角形的判定方法;理解坐标与图形的性质,记住两点间的距离公式;会运用分类讨论的思想解决数学问题.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
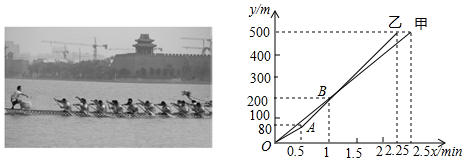
| A. | 乙队比甲队提前0.25min到达终点 | |
| B. | 当乙队划行110m时,此时落后甲队15m | |
| C. | 0.5min后,乙队比甲队每分钟快40m | |
| D. | 自1.5min开始,甲队若要与乙队同时到达终点,甲队的速度需要提高到255m/min |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
“春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
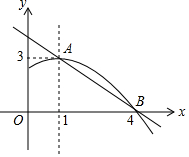 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-2),B(-2,-4),C(-4,-1).
如图,在平面直角坐标系中,△ABC的三个顶点分别为A(-1,-2),B(-2,-4),C(-4,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com