
如图,反比例函数y=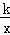 (k为常数,且k≠0)经过点A(1,3).
(k为常数,且k≠0)经过点A(1,3).
(1)求反比例函数的解析式;
(2)在x轴正半轴上有一点B,若△AOB的面积为6,求直线AB的解析式.



科目:初中数学 来源: 题型:
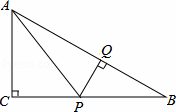
在Rt△ABC中,∠C=90°,P是BC边上不同于B、C的一动点,过P作PQ⊥AB,垂足为Q,连接AP.
(1)试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似;
(2)若AC=3,BC=4,当BP为何值时,△AQP面积最大,并求出最大值;
(3)在Rt△ABC中,两条直角边BC、AC满足关系式BC=λAC,是否存在一个λ的值,使Rt△AQP既与Rt△ACP全等,也与Rt△BQP全等.


查看答案和解析>>
科目:初中数学 来源: 题型:
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=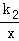 (k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为( )
(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为( )
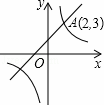
|
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 以上说法都不对 |


查看答案和解析>>
科目:初中数学 来源: 题型:
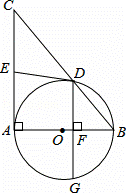
如图,AB为⊙O的直径,以AB为直角边作Rt△ABC,∠CAB=90°,斜边BC与⊙O交于点D,过点D作⊙O的切线DE交AC于点E,DG⊥AB于点F,交⊙O于点G.
(1)求证:E是AC的中点;
(2)若AE=3,cos∠ACB=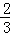 ,求弦DG的长.
,求弦DG的长.


查看答案和解析>>
科目:初中数学 来源: 题型:
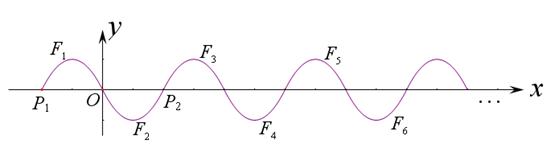
如图,抛物线 (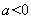 )位于
)位于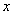 轴上方的图象记为
轴上方的图象记为 1 ,它与
1 ,它与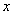 轴交于
轴交于 1 、
1 、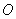 两点,图象
两点,图象 2与
2与 1关于原点
1关于原点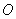 对称,
对称,  2与
2与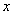 轴的另一个交点为
轴的另一个交点为 2 ,将
2 ,将 1与
1与 2同时沿
2同时沿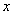 轴向右平移
轴向右平移 1
1 2的长度即可得
2的长度即可得 3与
3与 4 ;再将
4 ;再将 3与
3与 4 同时沿
4 同时沿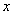 轴向右平移
轴向右平移 1
1 2的长度即可得
2的长度即可得 5与
5与 6 ; ……按这样的方式一直平移下去即可得到一系列图象
6 ; ……按这样的方式一直平移下去即可得到一系列图象 1 ,
1 , 2 ,…… ,
2 ,…… , n ,我们把这组图象称为“波浪抛物线”.
n ,我们把这组图象称为“波浪抛物线”.
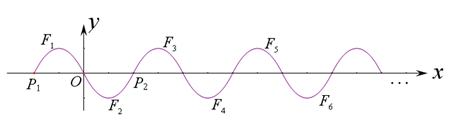
⑴ 当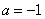 时,
时,
① 求图象 1的顶点坐标;
1的顶点坐标;
② 点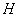 (2014 , -3) (填“在”或“不在”)该“波浪抛物线”上;若图象
(2014 , -3) (填“在”或“不在”)该“波浪抛物线”上;若图象 n 的顶点
n 的顶点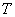 n的横坐标为201,则图象
n的横坐标为201,则图象 n 对应的解析式为______ ,其自变量
n 对应的解析式为______ ,其自变量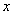 的取值范围为_______.
的取值范围为_______.
⑵ 设图象 m、
m、 m+1的顶点分别为
m+1的顶点分别为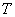 m 、
m 、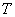 m+1 (m为正整数),
m+1 (m为正整数),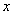 轴上一点Q的坐标为(12 ,0).试探究:当
轴上一点Q的坐标为(12 ,0).试探究:当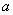 为何值时,以
为何值时,以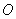 、
、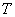 m 、
m 、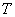 m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.
m+1、Q四点为顶点的四边形为矩形?并直接写出此时m的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com