
分析 分式的混合运算,先乘方,再乘除,然后加减,有括号的先算括号里面的,运算的结果要化成最简分式或整式.
解答 解:(1)原式=$\frac{2a}{a-1}$-$\frac{2(a-2)}{(a+1)(a-1)}$×$\frac{(a+1)^{2}}{a-2}$
=$\frac{2a}{a-1}$-$\frac{2(a+1)}{a-1}$
=$\frac{2a-2a-2}{a-1}$
=-$\frac{2}{a-1}$;
(2)原式=$\frac{x+1}{x}$÷$\frac{2{x}^{2}-1-{x}^{2}}{x}$
=$\frac{x+1}{x}$×$\frac{x}{{x}^{2}-1}$
=$\frac{x+1}{x}$×$\frac{x}{(x+1)(x-1)}$
=$\frac{1}{x-1}$;
(3)原式=[$\frac{2}{(a+b)(a-b)}$-$\frac{1}{a(a-b)}$]×$\frac{a+b}{a}$
=$\frac{2a-a-b}{a(a+b)(a-b)}$×$\frac{a+b}{a}$
=$\frac{a-b}{a(a+b)(a-b)}$×$\frac{a+b}{a}$
=$\frac{1}{{a}^{2}}$;
(4)原式=$\frac{3(a-1)}{a}$×$\frac{{a}^{2}}{(a-1)^{2}}$-$\frac{a}{a-1}$
=$\frac{3a}{a-1}$-$\frac{a}{a-1}$
=$\frac{3a-a}{a-1}$
=$\frac{2a}{a-1}$.
点评 本题主要考查了分式的混合运算,解决问题的关键是掌握分式的混合运算的顺序.分式的混合运算,一般按常规运算顺序,但有时应先根据题目的特点,运用乘法的运算律运算,会简化运算过程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 12 | 5 | 0 | -3 | -4 | -3 | 0 | 5 | 12 |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
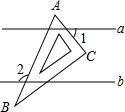 如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )
如图,直线a∥b,一块含60°角的直角三角板ABC(∠A=60°)按如图所示放置.若∠1=55°,则∠2的度数为( )| A. | 115° | B. | 110° | C. | 105° | D. | 100° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com