
【题目】长方形OABC在平面直角坐标系内的位置如图所示,将长方形沿BO折叠,使点C落在点D处,DO与AB交于点E,BC=4cm,BA=8cm,则点E的坐标为( ) 
A.(﹣3,4)
B.(﹣3.5,4)
C.(﹣3.7,4)
D.(﹣4,4)
【答案】A
【解析】解:∵四边形OABC是矩形, ∴∠OAB=90°,OA=BC=4cm,AB∥OC,
∴∠EBO=∠BOC,
由折叠的性质得:∠EOB=∠BOC,
∴∠EBC=∠EOB,
∴OE=BE,
设AE=x,则OE=BE=8﹣x,
在Rt△OAE中,由勾股定理得:AE2+OA2=OE2 ,
即x2+42=(8﹣x)2 ,
解得:x=3,
∴AE=3,
∴点E的坐标为(﹣3,4);
故选:A.
【考点精析】本题主要考查了矩形的性质和翻折变换(折叠问题)的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】与 ![]() 在平
在平![]() 面直角坐标系中的位置如图.
面直角坐标系中的位置如图.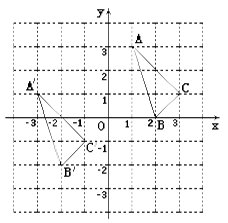
(1)分别写出下列各点的坐标:![]() ;
; ![]() ;
; ![]() ;
;
(2)说明 ![]() 由
由 ![]() 经过怎样的平移得到:
经过怎样的平移得到:
.
(3)若点 ![]() (
( ![]() ,
, ![]() )是
)是 ![]() 内部一点,则平移后
内部一点,则平移后 ![]() 内的
内的
对应点 ![]() 的坐标为;
的坐标为;
(4)求 ![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B两点在直线1的同侧,点A′与A关于直线l对称,连接A′B交l于点P.若A′B=a。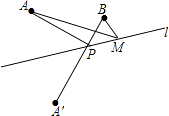
(1)求AP+PB。
(2)若点M是直线l上异于点P的任意一点,求证:AM+MB>AP+PB。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为支援灾区,某校爱心活动小组准备用筹集的资金购买A、B两种型号的学习用品共1000件.已知B型学习用品的单价比A型学习用品的单价多10元,用180元购买B型学习用品的件数与用120元购买A型学习用品的件数相同.
(1)求A、B两种学习用品的单价各是多少元?
(2)若购买这批学习用品的费用不超过28000元,则最多购买B型学习用品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,它表示甲乙两人从同一个地点出发后的情况.到十点时,甲大约走了13千米.根据图象回答: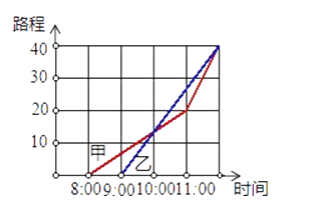
(1)甲是几点钟出发?
(2)乙是几点钟出发,到十点时,他大约走了多少千米?
(3)到十点为止,哪个人的速度快?
(4)两人最终在几点钟相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都为1,点A点B在网格中的位置如图所示.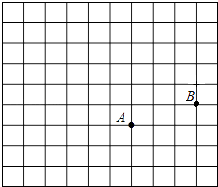
(1)建立适当的平面直角坐标系,使点A点B的坐标分别为(1,2)(4,3);
(2)点C的坐标为(3,6),在平面直角坐标系中找到点C的位置,连接AB、BC、CA,则∠ACB=°;
(3)将点A、B、C的横坐标都乘以﹣1,纵坐标不变,分别得到点A1、B1、C1 , 在图中找到点A1、B1、C1并顺次连接点A1、B1、C1 , 得到△A1B1C1 , 则这两个三角形关于对称.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B,P在一条直线上,则下列等式中,能判断点P是线段AB中点个数有 ( )
①AP=BP;②.BP= ![]() AB;③AB=2AP;④AP+PB=AB.
AB;③AB=2AP;④AP+PB=AB.
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D是BC边上的中点,∠BDE=∠CDF,请你添加一个条件,使DE=DF成立.你添加的条件是 . (不再添加辅助线和字母) 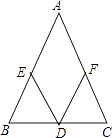
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com