

分析 (1)利用非负性和二次根式的意义得出结论;
(2)分两种情况讨论计算,分别表示出OP和OP',最后用面积公式即可,
(3)分两种情况求出满足条件的时间t,进而OQ和OQ'最后用面积公式即可得出结论.
解答 解:∵$\sqrt{-(a+2)^{2}}$-(b-6)2=0.
∴$\left\{\begin{array}{l}{a=-2}\\{b=6}\end{array}\right.$,
∴A(-2,0),B(0,6);
∴OA=2,OB=6;
(2)如图1,
∵OB=6,
∴t=6÷2=3,
①当点P在y轴正半轴上时,即:0<t<3,
由运动知,BP=2t,
∵OA=2,
∴OP=OB-BP=6-2t,
∴S=S△AOP=$\frac{1}{2}$OA•OP=$\frac{1}{2}$×2OP=OP=6-2t,
②当点P在y轴负半轴时,即:t>3,
由运动知,BP'=2t,
∴OP'=BP'-OB=2t-6,
∴S=S△AOP'=$\frac{1}{2}$OA•OP'=$\frac{1}{2}$×2OP'=OP'=2t-6,
即:S=$\left\{\begin{array}{l}{6-2t(0<t<3)}\\{2t-6(t>3)}\end{array}\right.$,
(3)如图2,
①当0<t<3时,∵S△AOP=4,
∴6-2t=4,
∴t=1,
∴点Q从A点沿x轴正方向1秒,OP=6-2=4,
∴AQ=1,
∵OA=2,
∴OQ=1,
∴S△APQ=$\frac{1}{2}$OQ•OP=$\frac{1}{2}$×OP=2;
S四边形ABPQ=S△AOB-S△POQ=$\frac{1}{2}$×OA×OB-$\frac{1}{2}$OQ×OP=6-$\frac{1}{2}$×1×4=4,
∴△APQ与以A、B、P、Q为顶点的四边形的面积之比1:2;
②当t>3时,∵S△AOP=4,
∴2t-6=4,
∴t=5,
∴点Q从A点沿x轴正方向5秒,OP'=4,AQ'=5,
∵OA=2,
∴OQ'=AQ'-OA=3,
∴S△AP'Q'=$\frac{1}{2}$OQ'•OP'=$\frac{1}{2}$×3×4=6,
∴S四边形ABQ'P'=S△AP'Q'+S△ABQ'=6+$\frac{1}{2}$×3×4=6+6=12,
∴△AP'Q'与以A、B、P'、Q'为顶点的四边形的面积之比1:2;
∴当S△AOP=4时,S△APQ的值为2或6.△APQ与以A、B、P、Q为顶点的四边形的面积之比1:2
点评 此题是三角形综合题,主要考查了非负性,三角形的面积公式,解本题的关键是分类讨论思想,是一道比较简单的题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
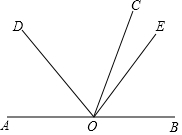 已知O为直线AB上一点,射线OD,OC,OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=80°.
已知O为直线AB上一点,射线OD,OC,OE位于直线AB上方,OD在OE的左侧,∠AOC=120°,∠DOE=80°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).
将直角边长为6的等腰直角△AOC放在平面直角坐标系中,点O为坐标原点,点C、A分别在x轴,y轴的正半轴上,一条抛物线经过点A、C及点B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于点D,在BC上取一点E,使得∠BAD=∠CAE,在AE上存在一点K,使得∠KBC=2∠BQD,求证:QK平分∠BKC.
如图,在△ABC中,AQ平分∠BAC,QD⊥BC交BC于点D,在BC上取一点E,使得∠BAD=∠CAE,在AE上存在一点K,使得∠KBC=2∠BQD,求证:QK平分∠BKC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=-$\frac{3}{4}$x+3的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C(2,n),过点C作CD⊥x轴,垂足为D.
如图,一次函数y=-$\frac{3}{4}$x+3的图象与x轴,y轴分别交于A,B两点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点C(2,n),过点C作CD⊥x轴,垂足为D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com