
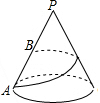
 已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号)
已知圆锥底面半径为1,母线长为4,地面圆周上有一点A,一只蚂蚁从点A出发沿圆锥侧面运动一周后到达母线PA中点B,则蚂蚁爬行的最短路程为2$\sqrt{5}$(结果保留根号) 分析 要求蚂蚁爬行的最短距离,需将圆锥的侧面展开,进而根据“两点之间线段最短”得出结果
解答 解:根据题意,将该圆锥展开如下图所示的扇形,
则,线段AB就是蚂蚁爬行的最短距离.
因为,圆锥的底面缘的周长=扇形的弧长,
所以,扇形的弧长l=2πr=2π,
扇形的半径=母线长,
由公式:l=$\frac{nπr}{180}$ 得,
圆心角 n=$\frac{180×2π}{4π}$=90°,
在RT△APM中,
AB=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
所以 蚂蚁爬行的最短路程为2$\sqrt{5}$,
故答案为:2$\sqrt{5}$,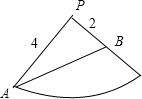
点评 此题是平面展开图--最短路程问题,考查了圆锥的侧面展开图是一个扇形,此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.本题就是把圆锥的侧面展开成扇形,“化曲面为平面”,用勾股定理解决.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{6}$ | B. | $\sqrt{8}$÷$\sqrt{2}$=4 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | (-$\sqrt{2}$)2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
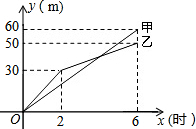 有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:
有两段长度相等的路面铺设任务,分别交给甲、乙两个施工队同时进行施工,甲、乙两个施工队铺设路面的长度y(米)与施工时间x(时)之间的函数关系的部分图象如图所示,下列四种说法:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $-\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com