
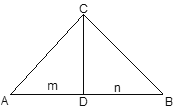
【题目】如图,已知△ABC中,∠ACB=90°,过C点作CD⊥AB,垂足为D,且AD=m,BD= n,AC2:BC2=2:1,又关于x的方程![]() x2-2(n-1)x+m2-12=0,两实数根的差的平方小于192,
x2-2(n-1)x+m2-12=0,两实数根的差的平方小于192,
求:m,n为整数时,一次函数y=mx+n的解析式.
【答案】当n=1,m=2时,所求解析式为y=2x+1;当n=2,m=4时,解析式为y=4x+2.
【解析】
由题意得到△ABC∽△ACD,根据△ABC∽△ACD,求出m和n之间的关系式;再根据根与系数的关系求出m、n的取值范围,然后估算,即可求得一次函数的解析式.
过C点作CD⊥AB,垂足为D,则∠CDA=90°,又因为∠ACB=90°, ∠CDA=∠ACB,则故△ABC∽△ACD,根据相似三角形的性质可得![]() ,AC2=ADAB;同理可得△ABC∽△BCD,则
,AC2=ADAB;同理可得△ABC∽△BCD,则![]() ,故BC2=BDAB,∵
,故BC2=BDAB,∵![]() ,∴
,∴![]() ,∴m=2n…①,
,∴m=2n…①,
∵关于x的方程![]() x2-2(n-1)x+m2-12=0有两实数根,
x2-2(n-1)x+m2-12=0有两实数根,
∴△=[-2(n-1)]2-4×![]() ×(m2-12)≥0,
×(m2-12)≥0,
∴4n2-m2-8n+16≥0,把①代入上式得n≤2…②,
设关于x的方程![]() x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
x2-2(n-1)x+m2-12=0的两个实数根分别为x1,x2,
则x1+x2=8(n-1),x1x2=4(m2-2),
依题意有(x1-x2)2<192,即[8(n-1)]2-16(m2-12)<192,
∴4n2-m2-8n+4<0,把①式代入上式得n>![]() …③,由②、③得
…③,由②、③得![]() <n≤2,
<n≤2,
∵m、n为整数,∴n的整数值为1,2,
当n=1,m=2时,所求解析式为y=2x+1;当n=2,m=4时,解析式为y=4x+2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.

(Ⅰ)如图①,当点D落在BC边上时,求点D的坐标;
(Ⅱ)如图②,当点D落在线段BE上时, AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(Ⅲ)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.则下列结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP.其中正确的是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“湖田十月清霜堕,晚稻初香蟹如虎”,又到了食蟹的好季节啦!某经销商去水产批发市场采购牟山湖大闸蟹,他看中了![]() 两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
两家的某种品质相近的大闸蟹.零售价都为80元/千克,批发价各不相同.
![]() 家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
家规定:批发数量不超过100千克,按零售价的92%优惠;批发数量超过100千克但不超过200千克,按零售价的90%优惠;超过200千克的按零售价的88%优惠.
B家的规定如下表:
数量范围(千克) | 0-50部分 | 50以上-150的部分 | 150以上-250的部分 | 250以上的部分 |
价格(元) | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
(1)如果他批发70千克牟山湖大闸蟹,则他在![]() 两家批发分别需要多少元;
两家批发分别需要多少元;
(2)如果他批发![]() 千克牟山湖大闸蟹(
千克牟山湖大闸蟹(![]() ),请你分别用含字母
),请你分别用含字母![]() 的式子表示他在
的式子表示他在![]() 两家批发所需的费用;
两家批发所需的费用;
(3)现在他要批发180千克山湖大闸蟹,你能帮助他选择哪家批发更便宜吗.请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB= cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标为(1,2).
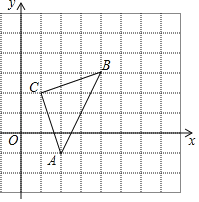
(1)写出点A,B的坐标:A( )、B( );
(2)判断△ABC的形状 ;计算△ABC的面积是 .
(3)将△ABC先向左平移2个单位长度,再向上平移1个单位长度,得到![]() ,则
,则![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ( ),
( ),![]() ( ),
( ),![]() ( ).
( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com