
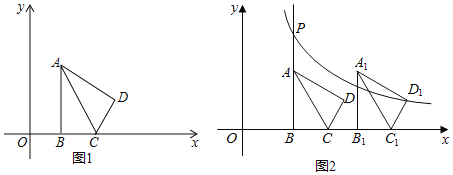
【题目】如图1,在平面直角坐标系xOy中,已知△ABC,∠ABC=90°,顶点A在第一象限,B,C在x轴的正半轴上(C在B的右侧),BC=2,AB=2![]() ,△ADC与△ABC关于AC所在的直线对称.
,△ADC与△ABC关于AC所在的直线对称.
(1)当OB=2时,求点D的坐标;
(2)若点A和点D在同一个反比例函数的图象上,求OB的长;
(3)如图2,将第(2)题中的四边形ABCD向右平移,记平移后的四边形为A1B1C1D1,过点D1的反比例函数y=![]() (k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
(k≠0)的图象与BA的延长线交于点P.问:在平移过程中,是否存在这样的k,使得以点P,A1,D为顶点的三角形是直角三角形?若存在,请直接写出所有符合题意的k的值;若不存在,请说明理由.
【答案】(1)点D坐标为(5,![]() );(2)OB=3;(3)k=12
);(2)OB=3;(3)k=12![]() .
.
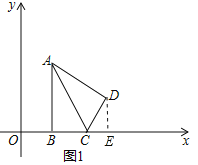
【解析】(1)如图1中,作DE⊥x轴于E,解直角三角形清楚DE,CE即可解决问题;
(2)设OB=a,则点A的坐标(a,2![]() ),由题意CE=1.DE=
),由题意CE=1.DE=![]() ,可得D(3+a,
,可得D(3+a,![]() ),点A、D在同一反比例函数图象上,可得2
),点A、D在同一反比例函数图象上,可得2![]() a=
a=![]() (3+a),求出a的值即可;
(3+a),求出a的值即可;
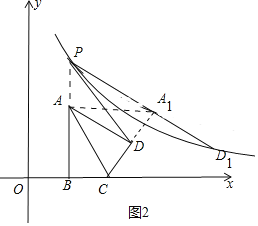
(3)分两种情形:①如图2中,当∠PA1D=90°时.②如图3中,当∠PDA1=90°时.分别构建方程解决问题即可;
(1)如图1中,作DE⊥x轴于E.
∵∠ABC=90°,
∴tan∠ACB=![]() ,
,
∴∠ACB=60°,
根据对称性可知:DC=BC=2,∠ACD=∠ACB=60°,
∴∠DCE=60°,
∴∠CDE=90°-60°=30°,
∴CE=1,DE=![]() ,
,
∴OE=OB+BC+CE=5,
∴点D坐标为(5,![]() ).
).
(2)设OB=a,则点A的坐标(a,2![]() ),
),
由题意CE=1.DE=![]() ,可得D(3+a,
,可得D(3+a,![]() ),
),
∵点A、D在同一反比例函数图象上,
∴2![]() a=
a=![]() (3+a),
(3+a),
∴a=3,
∴OB=3.
(3)存在.理由如下:
①如图2中,当∠PA1D=90°时.
∵AD∥PA1,
∴∠ADA1=180°-∠PA1D=90°,
在Rt△ADA1中,∵∠DAA1=30°,AD=2![]() ,
,
∴AA1=![]() =4,
=4,
在Rt△APA1中,∵∠APA1=60°,
∴PA=![]() ,
,
∴PB=![]() ,
,
设P(m,![]() ),则D1(m+7,
),则D1(m+7,![]() ),
),
∵P、A1在同一反比例函数图象上,
∴![]() m=
m=![]() (m+7),
(m+7),
解得m=3,
∴P(3,![]() ),
),
∴k=10![]() .
.
②如图3中,当∠PDA1=90°时.
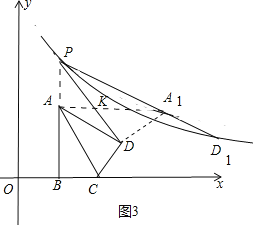
∵∠PAK=∠KDA1=90°,∠AKP=∠DKA1,
∴△AKP∽△DKA1,
∴![]() .
.
∴![]() ,
,
∵∠AKD=∠PKA1,
∴△KAD∽△KPA1,
∴∠KPA1=∠KAD=30°,∠ADK=∠KA1P=30°,
∴∠APD=∠ADP=30°,
∴AP=AD=2![]() ,AA1=6,
,AA1=6,
设P(m,4![]() ),则D1(m+9,
),则D1(m+9,![]() ),
),
∵P、A1在同一反比例函数图象上,
∴4![]() m=
m=![]() (m+9),
(m+9),
解得m=3,
∴P(3,4![]() ),
),
∴k=12![]() .
.


科目:初中数学 来源: 题型:
【题目】(知识生成)我们已经知道,多项式的乘法可以利用图形的面积进行解释.例如利用图1的面积可以得到![]() ,基于此,请解答下列问题:
,基于此,请解答下列问题:
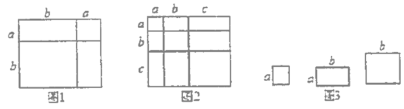
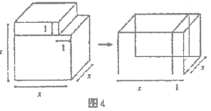
(1)请你写出图2所表示的一个等式:________.
(2)小明同学用图3中![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张宽、长分别为
张宽、长分别为![]() 、
、![]() 的长方形纸片拼出一个面积为
的长方形纸片拼出一个面积为![]() 长方形,则
长方形,则![]() ________.
________.
(知识迁移)(3)事实上,通过计算几何图形的体积也可以表示一些等式,图4表示的是一个边长为![]() 的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:________.
的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,.过B作BE//AC.
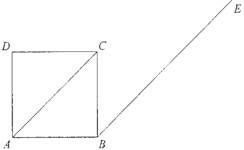
(1)求BE与AC之间的距离;
(2)F为BE上一点,连接AF,过C作CG//AF交BE于G.若∠FAB=15°,
①依题意补全图形;
②求证:四边形AFGC是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
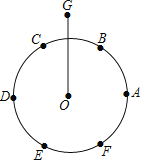
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A. ![]() r B. (1+
r B. (1+![]() )r C. (1+
)r C. (1+![]() )r D.
)r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点B,E,C,F在一条直线上,AC∥DE,∠A=∠D,AB=DF.
(1)试说明:△ABC≌△DFE;
(2)若BF=13,EC=7,求BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将矩形纸片![]() 沿对角线
沿对角线![]() 剪开,得到
剪开,得到![]() 和
和![]() .并且量得
.并且量得![]() ,
,![]() .
.
操作发现:
(1)将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转![]() ,使
,使![]() ,得到如图2所示的
,得到如图2所示的![]() ,过点
,过点![]() 作
作![]() 的平行线,与
的平行线,与![]() 的延长线交于点
的延长线交于点![]() ,则四边形
,则四边形![]() 的形状是________.
的形状是________.
(2)创新小组将图1中的![]() 以点
以点![]() 为旋转中心,按逆时针方向旋转,使
为旋转中心,按逆时针方向旋转,使![]() 、
、![]() 、
、![]() 三点在同一条直线上,得到如图3所示的
三点在同一条直线上,得到如图3所示的![]() ,连接
,连接![]() ,取
,取![]() 的中点
的中点![]() ,连接
,连接![]() 并延长至点
并延长至点![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,得到四边形
,得到四边形![]() ,发现它是正方形,请你证明这个结论.
,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将![]() 沿着
沿着![]() 方向平移,使点
方向平移,使点![]() 与点
与点![]() 重合,此时
重合,此时![]() 点平移至
点平移至![]() 点,
点,![]() 与
与![]() 相交于点
相交于点![]() ,如图4所示,连接
,如图4所示,连接![]() ,试求
,试求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )
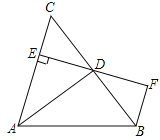
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,M、N、C三点的坐标分别为(![]() ,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作
,1),(3,1),(3,0),点A为线段MN上的一个动点,连接AC,过点A作![]() 交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
交y轴于点B,当点A从M运动到N时,点B随之运动,设点B的坐标为(0,b),则b的取值范围是( )
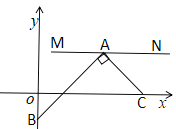
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是以O为圆心的半圆的直径,半径CO⊥AO,点M是![]() 上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
上的动点,且不与点A、C、B重合,直线AM交直线OC于点D,连结OM与CM.
(1)若半圆的半径为10.
①当∠AOM=60°时,求DM的长;
②当AM=12时,求DM的长.
(2)探究:在点M运动的过程中,∠DMC的大小是否为定值?若是,求出该定值;若不是,请说明理由.
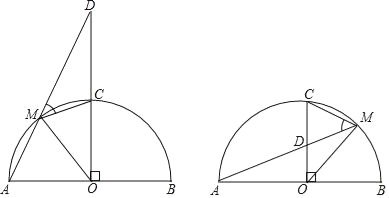
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com