
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
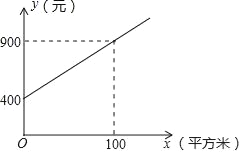
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,求证:AB=AC;
(2)如图2,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:如图①,∠C=∠ABD=∠E=90°,可知△ACB∽△BED.(不要求证明)
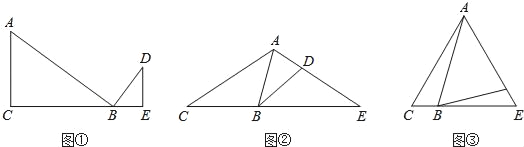
拓展:如图②,∠C=∠ABD=∠E.求证:△ACB∽△BED.
应用:如图③,∠C=∠ABD=∠E=60°,AC=4,BC=1,则△ABD与△BDE的面积比为
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示数20,点C表示数30,我们把数轴上两点之间的距离用表示两点的大写字母一起标记.
比如,点A与点B之间的距离记作AB,点B与点C之间的距离记作BC…
![]()
(1)点A与点C之间的距离记作AC,则AC的长为________;若数轴上有一点D满足CD=AD,则D点表示的数为___________;
(2)动点B从数1对应的点开始向右运动,速度为每秒1个单位长度,同时点A、C在数轴上运动,点A、C的速度分别为每秒2个单位长度,每秒3个单位长度,运动时间为t秒.
①若点A向右运动,点C向左运动,AB=BC,求t的值;
②若点A向左运动,点C向右运动,2ABm×BC的值不随时间t的变化而改变,则2ABm×BC的值为_____________(直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点B(6,8),动点M,N同时从O点出发,点M沿射线OA方向以每秒1个单位的速度运动,点N沿线段OB方向以每秒0.6个单位的速度运动,当点N到达点B时,点M,N同时停止运动,连接MN,设运动时间为t(秒).
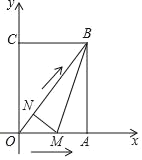
(1)求证△ONM~△OAB;
(2)当点M是运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点N,试求k的值;
的图象恰好过点N,试求k的值;
(3)△MNB与△OAB能否相似?若能试求出所有t的值,若不能请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
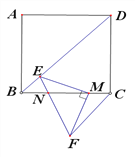
【题目】如图在正方形ABCD中,点M为BC边上一点,BM=4MC,以M为直角顶点作等腰直角三角形MEF,点E在对角线BD上,点F在正方形外EF交BC于点N,连CF,若BE=2,S△CMF=3,则MN=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
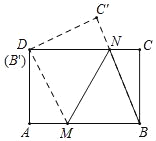
【题目】如图,四边形ABCD为矩形,将矩形ABCD沿MN折叠,折痕为MN,点B的对应点B′落在AD边上,已知AB=6,AD=4.
(1)若点B′与点D重合,连结DM,BN,求证:四边形BMB′N为菱形;
(2)在(1)问条件下求出折痕MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=![]() ,cosC=
,cosC=![]() .
.

(1)动手操作:利用尺规作以AC为直径的⊙O,并标出⊙O与AB的交点D,与BC的交点E(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证:弧DE=弧CE ;②求点D到BC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com