【答案】
分析:(1)利用表格数据可以得出月销售量P(千克)与月份x之间的函数关系式是一次函数关系:假设P=kx+b,利用图象上点的坐标为:(1,4500),(2,5000),利用待定系数法求出即可;
(2)利用上半年草莓的售价y(元/千克)与月份x之间满足一次函数关系
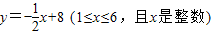
,得出W=Py=(500x+4000)(-

x+8),再利用二次函数的最值求法得出答案即可;
(3)首先求出能制成草莓酱质量,进而得出每份为:7000瓶,再利用已知批发价格表示出大型超市的零售价为:20(1+m%),大型商场的零售价为:20(1+m%)
2,进而得出7000×20(1+m%)+7000×20(1+m%)
2=35万,求出即可.
解答:解:(1)利用表格数据可以得出月销售量P(千克)与月份x之间的函数关系式是一次函数关系:
假设P=kx+b,图象上点的坐标为:(1,4500),(2,5000),
∴
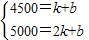
,
解得:
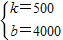
,
∴P=500x+4000;
(2)∵上半年草莓的售价y(元/千克)与月份x之间满足一次函数关系
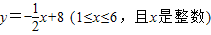
,
∴W=Py=(500x+4000)(-

x+8)
=-250x
2+2000x+32000,
当x=-
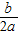
=-
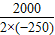
=4时,W
最大=
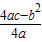
=36000元,
此时草莓的销售量为:P=500x+4000=500×4+4000=6000(kg);
(3)∵该种植基地今年收获了10000千克的草莓,并按(2)问中求出的销售量售出新鲜草莓.剩下的草莓与白糖、柠檬汁按4:2:1的比例制成草莓酱,
∴所剩草莓为:10000-6000=4000kg,
∴白糖、柠檬汁分别为:2000kg,1000kg;
∴制成草莓酱质量为:4000+2000+1000=7000kg,
∵草莓酱每瓶500克=0.5kg的方式装瓶出售,
∴草莓酱可以装成:7000÷0.5=14000瓶,
∵该基地将这批瓶装草莓酱平均分成两部分,
∴每份为:7000瓶,
∵每瓶草莓酱的批发价是20元,大型超市的零售价比批发价高m%,大型商场的零售价比超市的零售价又提高了m%.
∴大型超市的零售价为:20(1+m%),大型商场的零售价为:20(1+m%)
2,
∵该基地将这批瓶装草莓酱平均分成两部分,分别在大型超市、大型商场出售后销售总额达到了35万元,
∴7000×20(1+m%)+7000×20(1+m%)
2=35万,
整理得:2(1+m%)
2+2(1+m%)-5=0,
(m%)
2+3m%-1=0,
解得:m%=
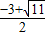
或
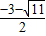
(不合题意舍去),
∵m%=
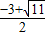
,
∴
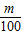
≈
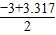
,
∴m≈16.
∴m的值为16.
点评:此题主要考查了二次函数的应用以及二次函数最值和一元二次方程的应用,根据已知得出草莓酱的瓶数以及利用在大型超市、大型商场出售后销售总额达到了35万元的出等式方程是解题关键.

 .月销售量P(千克)与月份x之间的相关数据如下表:
.月销售量P(千克)与月份x之间的相关数据如下表: )
)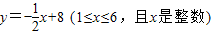 ,得出W=Py=(500x+4000)(-
,得出W=Py=(500x+4000)(- x+8),再利用二次函数的最值求法得出答案即可;
x+8),再利用二次函数的最值求法得出答案即可;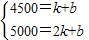 ,
,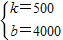 ,
,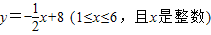 ,
, x+8)
x+8)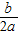 =-
=-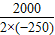 =4时,W最大=
=4时,W最大=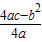 =36000元,
=36000元,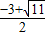 或
或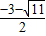 (不合题意舍去),
(不合题意舍去),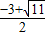 ,
,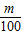 ≈
≈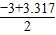 ,
,

 (2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表:
(2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表: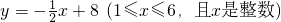 .月销售量P(千克)与月份x之间的相关数据如下表:
.月销售量P(千克)与月份x之间的相关数据如下表: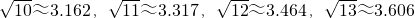 )
)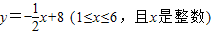 .月销售量P(千克)与月份x之间的相关数据如下表:
.月销售量P(千克)与月份x之间的相关数据如下表: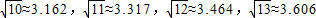 )
)