
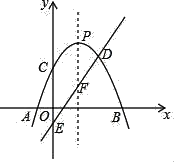
【题目】如图,抛物线L:y=﹣(x﹣2)2+m2+2m与x轴交于A,B,直线y=kx﹣1与y轴交于E,与L的对称轴交于点F(n,3),与L交于D,抛物线L的对称轴与L交于P.
(1)求k的值.
(2)点P能否与点F关于x轴的对称点重合?若认为能,请求出m的值;若认为不能,说明理由.
(3)小林研究了抛物线L的解析式后,得到了如下的结论:因为m可以取任意实数,所以点C可以在y轴上任意移动,即C点可以到达y轴的任何位置,你认为他说的有道理吗?说说你的想法.
(4)当抛物线L与直线y=kx﹣1有两个公共点时,直接写出适合条件的m的最大整数.
【答案】(1)k=2;(2)不能,理由见解析;(3)没道理,见解析;(4)适合条件的m的最大整数值是1.
【解析】
(1)首先得出对称轴方程,从而求得F点坐标,代入一次函数解析式,求k值;
(2)由对称点坐标关系可得点F关于x轴的对称点坐标,再与点P坐标比较,即可进行 判断;
(3)把L的解析式化成顶点式,就可以知道函数的最小值是-5,所以点C都不能到达(0,﹣5)以下的位置;
(4)两图像有公共点,即函数值相等,得到一元二次方程,
解:(1)抛物线L的对称轴是x=2,所以n=2,点F(2,3),代入y=kx﹣1中,得3=2k﹣1,
解得k=2;
(2)不能,理由:点P的坐标为(2,m2+2m),点F关于x轴的对称点F'的坐标是(2,﹣3),
若点P与点F'重合,则m2+2m=﹣3,
即:(m+1)2=﹣2.显然不可能;
(3)没道理,
因为,点C的纵坐标为yC=m2+2m﹣4=(m+1)2﹣5
因为yC的最小值为﹣5,所以无论m取何值,点C都不能到达(0,﹣5)以下的位置.
(4)直线y=kx﹣1的解析式为y=2x﹣1
当﹣(x﹣2)2+m2+2m=2x﹣1时,得x2﹣2x﹣(m2+2m﹣3)=0,
△=22﹣4×1×(m2+2m﹣3)=﹣4[(m+1)2﹣5]
当△≥0时,(m+1)2﹣5≤0,所以适合条件的m的最大整数值是1.


科目:初中数学 来源: 题型:
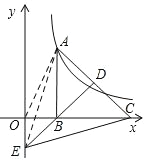
【题目】如图,Rt△ABC 的直角边 BC 在 x 轴的正半轴上,斜边 AC 边中线BD 的反向延长线交 y 轴负半轴于 E,双曲线 y=![]() (k>0)的图象经过点 A, 则△BEC 的面积为____(注:图中参考辅助线已给出)
(k>0)的图象经过点 A, 则△BEC 的面积为____(注:图中参考辅助线已给出)
查看答案和解析>>
科目:初中数学 来源: 题型:
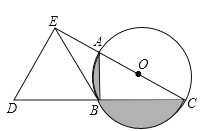
【题目】如图,AC为⊙O的直径,B为⊙O上一点,∠ACB=30°,延长CB至点D,使得CB=BD,过点D作DE⊥AC,垂足E在CA的延长线上,连接BE.
(1)求证:BE是⊙O的切线;
(2)当BE=3时,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
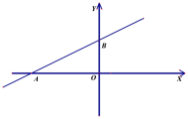
【题目】如图,在平面直角坐标系xOy中,O为坐标原点,已知直线![]() 经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB
(1)求直线![]() 的函数解析式
的函数解析式
(2)若直线![]() 也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
也经过点A(-6,0),且与y轴交于点C,如果ΔABC的面积为6,求C点的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:如图是华师版八年级上册数学教材第96页的部分内容.
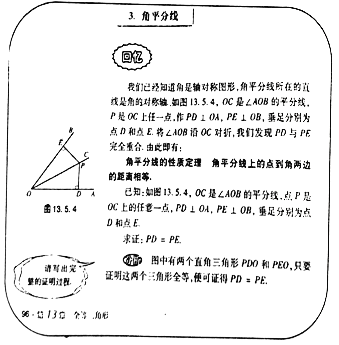

请根据教材中的分析,结合图①,写出“角平分线的性质定理”完整的证明过程.
定理应用:
如图②,在四边形ABCD中,∠B=∠C,点E在边BC上,AE平分∠BAD,DE平分∠ADC.
(1)求证:BE=CE.
(2)若四边形ABCD的周长为24,BE=2,面积为30,则△ABE的边AB的高的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某货运公司有大小两种货车,3辆大货车与4辆小货车一次可以运货29吨,2辆大货车与6辆小货车一次可以运货31吨.
(1)1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)有46.4吨货物需要运输,货运公司拟安排大小货车共10辆(要求两种货车都要用),全部货物一次运完,其中每辆大货车一次运货花费500元,每辆小货车一次运货花费300元,请问货运公司应如何安排车辆最节省费用?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1为放置在水平桌面上的台灯的平面示意图,灯臂AO长为50cm,与水平桌面所形成的夹角∠OAM 为75°.由光源O射出的边缘光线OC,OB 与水平桌面所形成的夹角∠OCA,∠OBA分别为90°和30°.(不考虑其他因素,结果精确到0.1cm.sin75°≈0.97,cos75°≈0.26,![]() ≈1.73)
≈1.73)
(1)求该台灯照亮水平桌面的宽度BC.
(2)有人在此台灯下看书,将其侧面抽象成如图2所示的几何图形,若书EF与水平桌面的夹角∠EFC为60°,书的长度EF为24cm,点P为眼睛所在位置,点P在EF的垂直平分线上,且到EF距离约为34cm,求眼睛到水平桌面的距离.
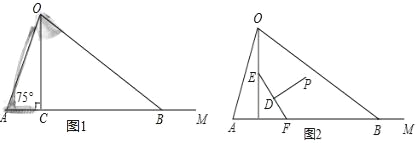
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形ABCD是边长为5的正方形,顶点A在y轴正半轴上,顶点B在x轴正半轴上,OA,OB的长满足|OA﹣4|+(OB﹣3)2=0.
(1)求OA,OB的长;
(2)求点D的坐标;
(3)在y轴上是否存在点P,使△PAB是以AB为腰的等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
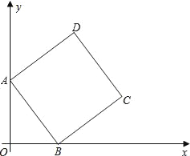
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com