
【题目】如图,△ABC中,∠C=90°,AC=BC=4,将△ABC翻折,使得点A落在BC的中点A'处,折痕分别交边AB、AC于点D、点E,那么AD:AE的值为_____.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,连接
,连接![]() .
.
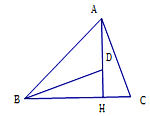
(1)求证:![]()
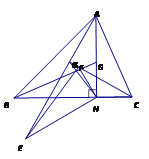
(2)如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() (点
(点![]() 分别对应点
分别对应点![]() ),设射线
),设射线![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,试探究线段
,试探究线段![]() 与
与![]() 之间满足的数量关系,并说明理由.
之间满足的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD、CF分别是∠BAC、∠ACB的角平分线,且AD、CF交于点I,IE⊥BC与E,下列结论:①∠BIE=∠CID;②S△ABC=![]() IE(AB+BC+AC);③BE=
IE(AB+BC+AC);③BE=![]() (AB+BC-AC);④AC=AF+DC.其中正确的结论是( )
(AB+BC-AC);④AC=AF+DC.其中正确的结论是( )

A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
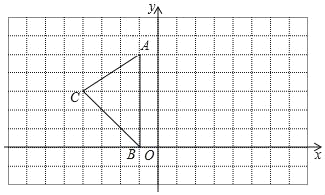
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3)
(1)在图中作出△ABC关于y轴的对称图形△A1B1C1;
(2)求出△A1B1C1的面积;
(3)将△ABC向左平移2个单位,再向上平移2个单位得△A2B2C2,请直接写出点A2,B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
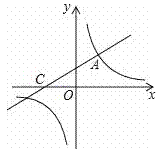
【题目】如图,直线![]() 与双曲线相交于点A(m,3),与x轴交于点C.
与双曲线相交于点A(m,3),与x轴交于点C.
(1)求双曲线解析式;
(2)点P在x轴上,如果△ACP的面积为3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年 7 月 1 日,《上海市生活垃圾管理条例》正式实施,生活垃圾按照“可回收物”、 “有害垃圾”、“湿垃圾”、“干垃圾”的分类标准.没有垃圾分类和未指定投放到指定垃圾桶内等会被罚款和行政处罚.垃圾分类制度即将在全国范围内实施,很多商家推出售卖垃圾分类桶,某商店经销垃圾分类桶.现有如下信息:
信息 1:一个垃圾分类桶的售价比进价高 12 元;
信息 2:卖 3 个垃圾分类桶的费用可进货该垃圾分类桶 4 个;
请根据以上信息,解答下列问题:
(1)该商品的进价和售价各多少元?
(2)商店平均每天卖出垃圾分类桶 16 个.经调查发现,若销售单价每降低 1 元,每天可多售出 2 个.为了使每天获取更大的利润,垃圾分类桶的售价为多少元时,商店每天获取的利润最大?每天的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com