
【题目】小华的爸爸要用一块矩形铁皮加工出一个底面半径为![]() ,高为
,高为![]() 的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
的锥形漏斗,要求只能有一条接缝(接缝忽略不计)
![]() 你能求出这个锥形漏斗的侧面展开图的圆心角吗?
你能求出这个锥形漏斗的侧面展开图的圆心角吗?
![]() 如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
如图,有两种设计方案,请你计算一下,哪种方案所用的矩形铁皮面积较少?
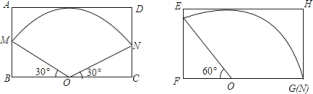
【答案】(1)120°(2)方案二所用的矩形铁皮面积较少
【解析】
(1)先根据勾股定理求出母线长为60,然后根据圆锥侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长和弧长公式计算锥形漏斗的侧面展开图的圆心角;(2)如图1,矩形的一边长等于母线长60,再利用含30度的直角三角形三边的关系计算出OB,从而得到BC长,再计算矩形ABCD的面积;如图2,矩形的一边长等于母线长60,再利用含30°的直角三角形三边的关系计算出OF,从而得到CG长,再计算矩形EFGH的面积,然后比较两矩形的面积即可.
![]() 圆锥的母线长
圆锥的母线长![]() ,
,
设这个锥形漏斗的侧面展开图的圆心角为![]() ,
,
所以![]() ,解得
,解得![]() ,
,
即这个锥形漏斗的侧面展开图的圆心角为![]() ;
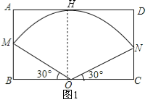
;![]() 如图
如图![]() ,
,![]() ,
,![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴方案一所需的矩形铁皮的面积![]() ,
,
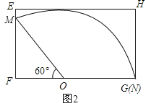
如图![]() ,
,![]() ,
,![]() ,
,
在![]() 中,∵
中,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴方案二所需的矩形铁皮的面积![]() ,
,
∴方案二所用的矩形铁皮面积较少.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A的纵坐标为2, 动点P沿路线![]() 运动.
运动.
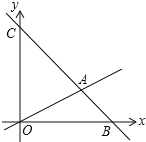
(1)求直线BC的解析式;
(2)在y轴上找一点M,使得△MAB的周长最小,则点M的坐标为______;(请直接写出结果)
(3)当△OPC的面积是△OAC的面积的![]() 时,求出这时P的坐标.
时,求出这时P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=![]() ,则经过点B(x,y)的反比例函数解析式为( )
,则经过点B(x,y)的反比例函数解析式为( )
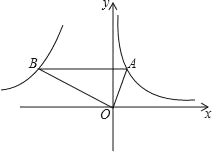
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
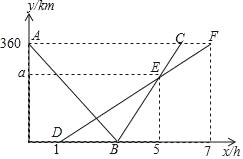
【题目】快、慢两车分别从相距360km的佳市、哈市两地出发,匀速行驶,先相向而行,慢车在快车出发1h后出发,到达佳市后停止行驶,快车到达哈市后,立即按原路原速返回佳市(快车调头的时间忽略不计),快、慢两车距哈市的路程y1(单位:km),y2(单位:km)与快车出发时间x(单位:h)之间的函数图象如图所示,请结合图象信息解答下列问题:
(1)直接写出慢车的行驶速度和a的值;
(2)快车与慢车第一次相遇时,距离佳市的路程是多少千米?
(3)快车出发多少小时后两车相距为100km?请直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 为的切线,
为的切线,![]() 、
、![]() 为切点,连接
为切点,连接![]() 、
、![]() ,
,![]() 交于点
交于点![]() ,
,![]() 交
交![]() 于
于![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,给出下列结论:①
,给出下列结论:①![]() ;②点
;②点![]() 为
为![]() 的内心;③
的内心;③![]() ;④
;④![]() ,其中正确的是( )
,其中正确的是( )
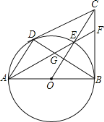
A. ① B. ①② C. ①②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(﹣1,5)、B(﹣1,0)、C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D、E、F分别是A、B、C的对应点).
(2)直接写出(1)中F点的坐标为 .
(3)若直线l经过点(0,﹣2)且与x轴平行,则点C关于直线l的对称点的坐标为 .
(4)在y轴上存在一点P,使PC﹣PB最大,则点P的坐标为 .
(5)第一象限有一点M(4,2),在x轴上找一点Q使CQ+MQ最短,画出最短路径,保留作图痕迹.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,AB=m,BC=6,点P为线段AD上任一点
(1)若∠BPC=60°,请在图中用尺规作图画出符合要求的点P;(保留作图痕迹,不要求写作法)
(2)若符合(1)中要求的点P必定存在,求m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批乒乓球的质量检验结果如下:
抽取的乒乓球数n | 200 | 500 | 1000 | 1500 | 2000 |
优等品频数m | 188 | 471 | 946 | 1426 | 1898 |
优等品频率 | 0.940 | 0.942 | 0.946 | 0.951 | 0.949 |
(1)画出这批乒乓球“优等品”频率的折线统计图;
(2)这批乒乓球“优等品”的概率的估计值是多少?
(3)从这批乒乓球中选择5个黄球、13个黑球、22个红球,它们除颜色外都相同,将它们放入一个不透明的袋中.
①求从袋中摸出一个球是黄球的概率;
②现从袋中取出若干个黑球,并放入相同数量的黄球,搅拌均匀后使从袋中摸出一个是黄球的概率不小于![]() , 问至少取出了多少个黑球?
, 问至少取出了多少个黑球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:
数学活动课上,李老师给出如下定义:如果一个三角形有一边上的中线等于这条边的一半,那么称三角形为“智慧三角形”.

理解:
⑴如图![]() ,已知
,已知![]() 是⊙
是⊙![]() 上两点,请在圆上找出满足条件的点
上两点,请在圆上找出满足条件的点![]() ,使
,使![]() 为“智慧三角形”(画出点
为“智慧三角形”(画出点![]() 的位置,保留作图痕迹);
的位置,保留作图痕迹);
⑵如图![]() ,在正方形
,在正方形![]() 中,
中,![]() 是
是![]() 的中点,
的中点,![]() 是
是![]() 上一点,且
上一点,且![]() ,试判断
,试判断![]() 是否为“智慧三角形”,并说明理由;
是否为“智慧三角形”,并说明理由;
运用:
⑶如图![]() ,在平面直角坐标系
,在平面直角坐标系![]() 中,⊙
中,⊙![]() 的半径为
的半径为![]() ,点
,点![]() 是直线
是直线![]() 上的一点,若在⊙
上的一点,若在⊙![]() 上存在一点
上存在一点![]() ,使得
,使得![]() 为“智慧三角形”,当其面积取得最小值时,直接写出此时点
为“智慧三角形”,当其面积取得最小值时,直接写出此时点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com