
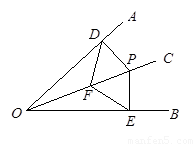
如图,OC是∠AOB的角平分线,P是OC上一点.PD⊥OA交OA于D,PE⊥OB交OB于E,F是OC上的另一点,连接DF,EF.求证:DF=EF.
证明见解析.
【解析】
试题分析:证明线段相等的方法一般是三角形的全等,找到包含两条线段的两个三角形△DPF和△EPF,然后找全等的条件,角平分线线上的点到两边的距离相等,所以PD=PE,因为PE⊥OB,PD⊥AO,所以∠PDO=
∠PEO=90°,所以∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,即∠DPF=∠EPF,在△DPF和△EPF中, PD=PE, ∠DPF=∠EPF,PF=PF,所以△DPF≌△EPF,所以DF=EF.
试题解析:∵点P在∠AOB的角平分线OC上,PE⊥OB,PD⊥AO,
∴PD=PE,∠DOP=∠EOP,∠PDO=∠PEO=90°,
∴∠DPF=90°-∠DOP,∠EPF=90°-∠EOP,
∴∠DPF=∠EPF,
在△DPF和△EPF中,
PD=PE, ∠DPF=∠EPF,PF=PF,
∴△DPF≌△EPF(ASA),
∴DF=EF.
考点:角平分线的性质和三角形的全等.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 13、如图,OC是∠AOB的平分线,点D是OC上的一点,DE⊥OA于点E,DF⊥OB于点F,连接EF,交OC于点P,把这个图形沿OC对折后观察,除∠AOC=∠BOC外,你还可以发现的结论是
13、如图,OC是∠AOB的平分线,点D是OC上的一点,DE⊥OA于点E,DF⊥OB于点F,连接EF,交OC于点P,把这个图形沿OC对折后观察,除∠AOC=∠BOC外,你还可以发现的结论是查看答案和解析>>
科目:初中数学 来源: 题型:
 22、(1)画出下图的三视图.
22、(1)画出下图的三视图.查看答案和解析>>
科目:初中数学 来源: 题型:
 25、如图,OC是∠AOB的平分线,且∠AOD=90°.
25、如图,OC是∠AOB的平分线,且∠AOD=90°.查看答案和解析>>
科目:初中数学 来源: 题型:
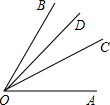 如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )
如图,OC是∠AOB的平分线,OD是∠BOC的平分线,那么下列各式中正确的是( )A、∠COD=
| ||
B、∠AOD=
| ||
C、∠BOD=
| ||
D、∠BOC=
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com