
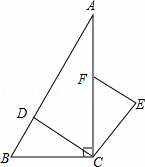
如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△ BCD≌△FCE;
BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
某服装商预测一种应季衬衫能畅销市场,就用8000元购进一批衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价都是100元,最后剩下10件按8折销售,很快售完.在这两笔生意中,商家共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,AB是半圆O的直径,D,E是半圆上任意两点,连结AD,DE,AE与BD相交于点C,要使△ADC与△ABD相似,可以添加一个条件.下列添加的条件其中错误的是( )

A. ∠ACD=∠DAB B.AD=DE C.AD2=BD•CD D. CD•AB=AC•BD
查看答案和解析>>
科目:初中数学 来源: 题型:
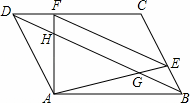
已知:如图,在平行四边形ABCD中,E、F分别是边BC,CD上的点,且EF∥BD,AE、AF分别交BD与点G和点H,BD=12,EF=8.求:
(1) 的值;
的值;
(2)线段GH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com