
【题目】如图,Rt△ABC中,∠C=90°,D为BC边上一动点,过D作DE⊥AD交AB于E,AC=2,BC=4,当D点从C点运动到B点时,点E运动的路径长为_____.
科目:初中数学 来源: 题型:
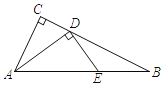
【题目】已知四边形![]() 和四边形
和四边形![]() 都是正方形,且
都是正方形,且![]() .
.
(1)如图1,连接![]() 、
、![]() .求证:
.求证:![]() ;
;
(2)如图2,如果正方形![]() 绕点
绕点![]() 旋转到某一位置恰好使得
旋转到某一位置恰好使得![]() ,
,![]() .
.
①求![]() 的度数;
的度数;
②若正方形![]() 的边长是
的边长是![]() ,请求出
,请求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
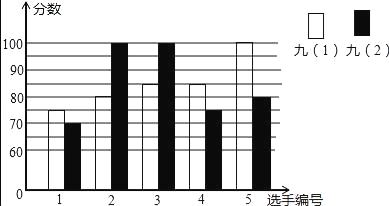
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果一个一元二次方程的两个实数根的比值与另一个一元二次方程的两个实数根的比值相等,我们称这两个方程为“相似方程”,例如,![]() 的实数根是3或6,
的实数根是3或6,![]() 的实数根是1或2,
的实数根是1或2,![]() ,则一元二次方程
,则一元二次方程![]() 与
与![]() 为相似方程.下列各组方程不是相似方程的是( )
为相似方程.下列各组方程不是相似方程的是( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
数学课上,李老师提出了这样一个问题:如图1,点![]() 是正方形
是正方形![]() 内一点,
内一点,![]() ,
,![]() ,
,![]() .你能求出
.你能求出![]() 的度数吗?
的度数吗?
(1)小敏与同桌小聪通过观察、思考、讨论后,得出了如下思路:
思路一:将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,求出
,求出![]() 的度数.
的度数.
思路二:将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() ,求出
,求出![]() 的度数.
的度数.
请参考以上思路,任选一种写出完整的解答过程.
类比探究
(2)如图2,若点![]() 是正方形
是正方形![]() 外一点,
外一点,![]() ,
,![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
拓展应用
(3)如图3,在边长为![]() 的等边三角形
的等边三角形![]() 内有一点
内有一点![]() ,
,![]() ,
,![]() ,则
,则![]() 的面积是______.
的面积是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进A、B两种商品进行销售,每次购进同一种商品的进价相同,具体情况如下表所示:
(1)求A、B两种商品每件的进价分别是多少元?
(2)商店计划用5300元的资金进行第三次进货,共进A、B两种商品100件,其中要求B商品的数量不少于A商品的数量,有几种进货方案?
(3)综合考虑(2)的情况,商店计划对第三次购进的100件商品全部销售,A商品售价为30元/件,每销售一件A商品需捐款a元(1≤a≤10)给希望工程,B商品售价为100元/件,每销售一件B商品需捐款b元给希望工程,a+b=14.直接写出当b= 时,销售利润最大,最大利润为 元.

查看答案和解析>>
科目:初中数学 来源: 题型:
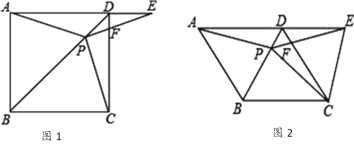
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F.
(1)证明:△APD≌△CPD;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=120°时,连接CE,试探究线段AP与线段CE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程.
已知:⊙O及⊙O外一点P.
求作:直线PA和直线PB,使PA切⊙O于点A,PB切⊙O于点B.
作法:如图,
①连接OP,分别以点O和点P为圆心,大于![]() OP的同样长为半径作弧,两弧分别交于点M,N;
OP的同样长为半径作弧,两弧分别交于点M,N;
②连接MN,交OP于点Q,再以点Q为圆心,OQ的长为半径作弧,交⊙O于点A和点B;
③作直线PA和直线PB.
所以直线PA和PB就是所求作的直线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
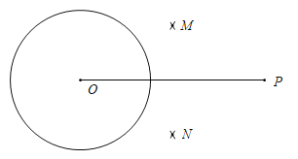
(2)完成下面的证明.
证明:∵OP是⊙Q的直径,
∴ ∠OAP=∠OBP=________°( )(填推理的依据).
∴PA⊥OA,PB⊥OB.
∵OA,OB为⊙O的半径,
∴PA,PB是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,点E是AB上一点,且AE=2EB .
(1)求![]() 的值.
的值.
(2)求![]() 的值.
的值.
(3)如果△AEF的面积![]() =8cm2,分别求出△CDF的面积
=8cm2,分别求出△CDF的面积![]() 和△ADF的面积
和△ADF的面积![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com