
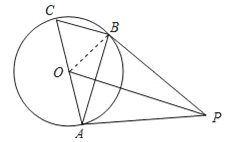
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
【答案】(1)详见解析;(2)BC=2.
【解析】试题分析:(1)连接OB,由圆周角定理得出∠ABC=90°,得出∠C+∠BAC=90°,再由OA=OB,得出∠BAC=∠OBA,证出∠PBA+∠OBA=90°,即可得出结论;
(2)证明△ABC∽△PBO,得出对应边成比例,即可求出BC的长.
试题解析:(1)证明:连接OB,如图所示:
∵AC是⊙O的直径,
∴∠ABC=90°,
∴∠C+∠BAC=90°,
∵OA=OB,
∴∠BAC=∠OBA,
∵∠PBA=∠C,
∴∠PBA+∠OBA=90°,
即PB⊥OB,
∴PB是⊙O的切线;
(2)解:∵⊙O的半径为2![]() ,
,
∴OB=2![]() ,AC=4
,AC=4![]() ,
,
∵OP∥BC,
∴∠C=∠BOP,
又∵∠ABC=∠PBO=90°,
∴△ABC∽△PBO,
∴![]() ,
,
即![]() ,
,
∴BC=2.


 智慧小复习系列答案
智慧小复习系列答案科目:初中数学 来源: 题型:
【题目】如图为放置在水平桌面上的台灯的平面示意图,灯臂AO长为40cm,与水平面所形成的夹角∠OAM为75°.由光源O射出的边缘光线OC,OB与水平面所形成的夹角∠OCA,∠OBA分别为90°和30°,求该台灯照亮水平面的宽度BC(不考虑其他因素,结果精确到0.1cm.温馨提示:sin75°≈0.97,cos75°≈0.26,![]() ≈1.73).
≈1.73).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若Rt△ABC的各边都扩大4倍,得到Rt△A′B′C′,则锐角∠A、∠A′的正弦值的关系为( )
A. sinA′=sinA B. 4sinA′=sinA C. sinA′=4sinA D. 不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D. 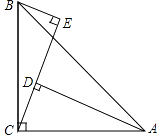
(1)求证:△ADC≌△CEB.
(2)AD=5cm,DE=3cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,已知A(6,0),B(8,6),将线段OA平移至CB,点D在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)写出点C的坐标;
(2)当△ODC的面积是△ABD的面积的3倍时,求点D的坐标;
(3)设∠OCD=α,∠DBA=β,∠BDC=θ,判断α、β、θ之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点在(3,0)和(4,0)之间.则下列结论:①
的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点在(3,0)和(4,0)之间.则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④一元二次方程
;④一元二次方程![]() 有两个不相等的实数根.其中正确结论的个数是( )
有两个不相等的实数根.其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com