
ЁОЬтФПЁПЮЊНЈЩшУРРіМвдАЃЌФГЩчЧјНЋЯНЧјФкЕФ-ПщУцЛ§ЮЊ1000m2ЕФПеЕиНјааТЬЛЏЃЌ-ВПЗжжжВнЃЌЪЃгрВПЗжддЛЈЃЌЩшжжВнВПЗжЕФУцЛ§ЮЊx(m2)ЃЌжжВнЫљашЗбгУyl(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЭМЯѓШчЭМЫљЪОЃЌддЛЈЫљашЗбгУy2(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЪНЮЊy2=-0.Olx2-20x+30000(0ЁмxЁм1000)ЃЎ
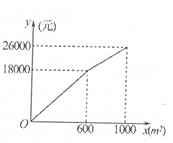
(1)Чѓyl(дЊ)гыx(m2)ЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)ЩшетПщ1000m2ПеЕиЕФТЬЛЏзмЗбгУЮЊW(дЊ)ЃЌЧыРћгУWгыxЕФКЏЪ§ЙиЯЕЪНЃЌЧѓТЬЛЏзмЗбгУWЕФзюДѓжЕЃЎ
ЁОД№АИЁП(1)МћНтЮіЃЛ(2)W=0.01x2+36000ЃЌWШЁзюДѓжЕЮЊ32500дЊ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнКЏЪ§ЭМЯѓРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓЕУy1ЃЈдЊЃЉгыxЃЈm2ЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉзмЗбгУЮЊW=y1+y2ЃЌСаГіКЏЪ§ЙиЯЕЪНМДПЩЧѓНт.
ЃЈ1ЃЉЕБ0x<600ЪБЃЌЩшКЏЪ§НтЮіЪНЮЊy1=k1xЃЌ
НЋx=600ЁЂy=18000ЕУЃК600k1=18000ЃЌ
НтжЎЃКk1=30ЃЌ
Ёрy1=30xЃЌ
ЕБ600x1000ЪБЃЌЩшy1=k2x+bЃЌ
НЋx=600ЁЂy=18000КЭx=1000ЁЂy=26000ДњШыЗжБ№ДњШыЕУЃК ЃЌ
ЃЌ
НтжЎЃК![]() ЃЌ
ЃЌ
Ёрy1=20x+6000ЃЌ
Ёр![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕБ0x<600ЪБЃЌ
W=30x+(0.01x220x+30000)=0.01x2+10x+30000ЃЌ
Ёп0.01<0ЃЌ
W=0.01(x500)2+32500ЃЌ
ЁрЕБx=500ЪБЃЌWШЁЕУзюДѓжЕЮЊ32500дЊЃЛ
ЕБ600x1000ЪБЃЌ
W=20x+6000+(0.01x220x+30000)=0.01x2+36000ЃЌ
Ёп0.01<0ЃЌ
ЁрЕБ600x1000ЪБЃЌWЫцxЕФдіДѓЖјМѕаЁЃЌ
ЁрЕБx=600ЪБЃЌWШЁзюДѓжЕЮЊ32400ЃЌ
Ёп32400<32500ЃЌ
ЁрWШЁзюДѓжЕЮЊ32500дЊ,,


 ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ
ЕуОІаТНЬВФШЋФмНтЖСЯЕСаД№АИ аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
аЁбЇНЬВФЭъШЋНтЖСЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌШєЁб
ЃЌШєЁб![]() ЕФдВаФдкЯпЖЮ
ЕФдВаФдкЯпЖЮ![]() ЩЯЃЌЧвЁб
ЩЯЃЌЧвЁб![]() гы
гы![]() ЖМЯрЧаЃЌдђЁб
ЖМЯрЧаЃЌдђЁб![]() ЕФАыОЖЪЧ___________ЃЎ
ЕФАыОЖЪЧ___________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
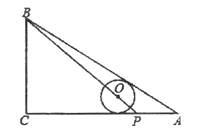
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌЁЯACB=90ЁуЃЌAC=4cmЃЌBC=6cmЃЌDЪЧBCЕФжаЕу.ЕуEДгAГіЗЂЃЌвдacm/s(aЃО0)ЕФЫйЖШбиACдШЫйЯђЕуCдЫЖЏЃЛЕуFЭЌЪБвд1cm/sЕФЫйЖШДгЕуCГіЗЂЃЌбиCBдШЫйЯђЕуBдЫЖЏЃЌЦфжавЛИіЖЏЕуЕНДяЖЫЕуЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙдЫЖЏЃЌЙ§ЕуEзїACЕФДЙЯпЃЌНЛADгкЕуGЃЌСЌНгEFЃЌFGЃЌЩшЫќУЧдЫЖЏЕФЪБМфЮЊtУы(tЁнt0).
(1)Шєt=2ЃЌЁїCEFЁзЁїABCЃЌЧѓaЕФжЕЃЛ
(2)ЕБa=![]() ЪБЃЌвдЕуEЁЂFЁЂDЁЂGЮЊЖЅЕуЕуЫФБпаЮЪБЦНааЫФБпаЮЃЌЧѓtЕФжЕЃЛ
ЪБЃЌвдЕуEЁЂFЁЂDЁЂGЮЊЖЅЕуЕуЫФБпаЮЪБЦНааЫФБпаЮЃЌЧѓtЕФжЕЃЛ
(3)Шєa=2ЃЌЪЧЗёДцдкЪЕЪ§tЃЌЪЙЕУЕуЁїDFGЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыЧѓГіtЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
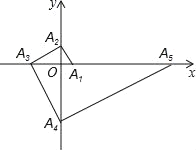
ЁОЬтФПЁПШчЭМЃЌЕуA1ЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌA2дкyжсЕФе§АыжсЩЯЃЌЧвЁЯA1A2OЃН30ЁуЃЌЙ§ЕуA2зїA2A3ЁЭA1A2ДЙзуЮЊA2ЃЌНЛxжсгкЕуA3Й§ЕуA3зїA3A4ЁЭA2A3ЃЌДЙзуЮЊA3ЃЌНЛyжсгкЕуA4ЃЌЙ§ЕуA4зїA4A5ЁЭA3A4ЃЌДЙзуЮЊA4ЁНЛxжсгкЕуA5ЃКЙ§ЕуA5зїA5A6ЁЭA4A5ЃЌA5A6ЁЭA4A5ДЙзуЮЊA5ЃЌНЛyжсгкЕуA6ЁАДДЫЙцТЩНјааЯТШЅЃЌдђЕуA2019ЕФКсзјБъЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=-x2+mxЕФЖдГЦжсЮЊжБЯпx=2ЃЌШєЙигкxЕФ-дЊЖўДЮЗНГЬ-x2+mx-t=0 (tЮЊЪЕЪ§)дкl<x<3ЕФЗЖЮЇФкгаНтЃЌдђtЕФШЁжЕЗЖЮЇЪЧ( )
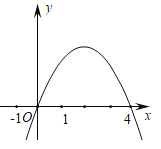
A.-5<tЁм4 B.3<tЁм4 C.-5<t<3 D.t>-5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
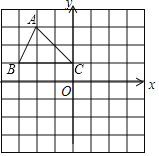
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁїABCШ§ИіЖЅЕуЖМдкИёЕуЩЯЃЌЕуAЃЌBЃЌCЕФзјБъЗжБ№ЮЊAЃЈЉ2ЃЌ3ЃЉЃЌBЃЈЉ3ЃЌ1ЃЉЃЌCЃЈ0ЃЌ1ЃЉЧыНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЁїABCгыЁїA1B1C1ЙигкдЕуOГЩжааФЖдГЦЃЌЛГіЁїA1B1C1ВЂжБНгаДГіЕуAЕФЖдгІЕуA1ЕФзјБъЃЛ
ЃЈ2ЃЉЛГіЁїABCШЦЕуCЫГЪБеыа§зЊ90ЁуКѓЕУЕНЕФЁїA2B2CЃЌВЂЧѓГіЯпЖЮACа§зЊЪБЩЈЙ§ЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПТцЭеБЛГЦЮЊЁАЩГФЎжЎжлЁБЃЌЫќЕФЬхЮТЫцЪБМфЕФБфЛЏЖјЗЂЩњНЯДѓБфЛЏЃЌЦфЬхЮТЃЈ![]() ЃЉгыЪБМфЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМ1ЫљЪОЃЎ
ЃЉгыЪБМфЃЈаЁЪБЃЉжЎМфЕФЙиЯЕШчЭМ1ЫљЪОЃЎ

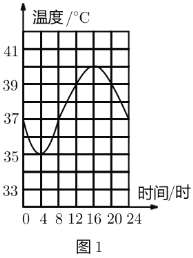
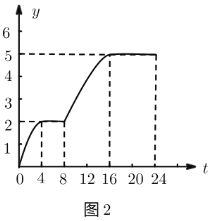
аЁЧхЭЌбЇИљОнЭМ1ЛцжЦСЫЭМ2ЃЌдђЭМ2жаЕФБфСПгаПЩФмБэЪОЕФЪЧЃЈ ЃЉЃЎ
A.ТцЭедк![]() ЪБПЬЕФЬхЮТгы0ЪБЬхЮТЕФОјЖдВюЃЈМДВюЕФОјЖджЕЃЉ
ЪБПЬЕФЬхЮТгы0ЪБЬхЮТЕФОјЖдВюЃЈМДВюЕФОјЖджЕЃЉ
B.ТцЭеДг0ЪБЕН![]() ЪБПЬжЎМфЕФзюИпЬхЮТгыЕБШезюЕЭЬхЮТЕФВю
ЪБПЬжЎМфЕФзюИпЬхЮТгыЕБШезюЕЭЬхЮТЕФВю
C.ТцЭедк![]() ЪБПЬЕФЬхЮТгыЕБШеЦНОљЬхЮТЕФОјЖдВю
ЪБПЬЕФЬхЮТгыЕБШеЦНОљЬхЮТЕФОјЖдВю
D.ТцЭеДг0ЪБЕН![]() ЪБПЬжЎМфЕФЬхЮТзюДѓжЕгызюаЁжЕЕФВю
ЪБПЬжЎМфЕФЬхЮТзюДѓжЕгызюаЁжЕЕФВю
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛЖЮХзЮяЯпyЃНЉx2+4ЃЈЉ2ЁмxЁм2ЃЉЮЊC1ЃЌгыxжсНЛгкA0ЃЌA1СНЕуЃЌЖЅЕуЮЊD1ЃЛНЋC1ШЦЕуA1а§зЊ180ЁуЕУЕНC2ЃЌЖЅЕуЮЊD2ЃЛC1гыC2зщГЩвЛИіаТЕФЭМЯѓЃЌДЙжБгкyжсЕФжБЯпlгыаТЭМЯѓНЛгкЕуP1ЃЈx1ЃЌy1ЃЉЃЌP2ЃЈx2ЃЌy2ЃЉЃЌгыЯпЖЮD1D2НЛгкЕуP3ЃЈx3ЃЌy3ЃЉЃЌЩшx1ЃЌx2ЃЌx3ОљЮЊе§Ъ§ЃЌtЃНx1+x2+x3ЃЌдђtЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
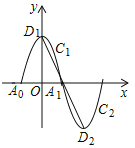
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌAB=![]() ЃЌEЪЧADБпЩЯЕФвЛЕу(ЕуEгыЕуAКЭЕуDВЛжиКЯ)ЃЌBEЕФДЙжБЦНЗжЯпНЛABгкЕуMЃЌНЛDCгкЕуN.
ЃЌEЪЧADБпЩЯЕФвЛЕу(ЕуEгыЕуAКЭЕуDВЛжиКЯ)ЃЌBEЕФДЙжБЦНЗжЯпНЛABгкЕуMЃЌНЛDCгкЕуN.
(1)жЄУїЃКMN = BE.
(2)ЩшAE=![]() ЃЌЫФБпаЮADNMЕФУцЛ§ЮЊSЃЌаДГіSЙигк
ЃЌЫФБпаЮADNMЕФУцЛ§ЮЊSЃЌаДГіSЙигк![]() ЕФКЏЪ§ЙиЯЕЪН.
ЕФКЏЪ§ЙиЯЕЪН.
(3)ЕБAEЮЊКЮжЕЪБЃЌЫФБпаЮADNMЕФУцЛ§зюДѓЃПзюДѓжЕЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com