
【题目】抛物线![]() (
(![]() 为常数)与
为常数)与![]() 轴交于点
轴交于点![]() 和
和![]() 与
与![]() 轴交于点
轴交于点![]() ,点
,点![]() 为抛物线顶点.
为抛物线顶点.
(Ⅰ)当![]() 时,求点
时,求点![]() ,点
,点![]() 的坐标;
的坐标;
(Ⅱ)①若顶点![]() 在直线
在直线![]() 上时,用含有
上时,用含有![]() 的代数式表示
的代数式表示![]() ;
;
②在①的前提下,当点![]() 的位置最高时,求抛物线的解析式;
的位置最高时,求抛物线的解析式;
(Ⅲ)若![]() ,当
,当![]() 满足
满足![]() 值最小时,求
值最小时,求![]() 的值.
的值.
【答案】(Ⅰ)![]() ;(Ⅱ)①
;(Ⅱ)①![]() ;②
;②![]() ;(Ⅲ)
;(Ⅲ)![]()
【解析】
(Ⅰ)当![]() 时,y=0,由二次函数的交点式即可求出解析式;
时,y=0,由二次函数的交点式即可求出解析式;
(Ⅱ)①由题意得![]() ,代入直线y=x中即可解答;
,代入直线y=x中即可解答;
②表达出![]() ,根据二次函数的性质可知,当b=1时,点A在最高点,即可得到二次函数解析式;
,根据二次函数的性质可知,当b=1时,点A在最高点,即可得到二次函数解析式;
(Ⅲ)将(-1,0)代入得到c=b+1,表达出![]() , A(0,b+1),求出点E关于x轴的对称点
, A(0,b+1),求出点E关于x轴的对称点![]() ,根据当
,根据当![]() 满足
满足![]() 值最小时,则此时点P,A,
值最小时,则此时点P,A,![]() 三点共线,求出直线AP的解析式,将点
三点共线,求出直线AP的解析式,将点![]() 代入直线AP的解析式即可求出b的值.
代入直线AP的解析式即可求出b的值.
解:(Ⅰ)当![]() 时,y=0,
时,y=0,
∴![]() ,
,
∴![]()
(Ⅱ)①∵点E是抛物线![]() 的顶点,
的顶点,
∴![]() ,
,
∵顶点![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,
∴![]() ,
,
②由①可知![]() ,
,
![]() ,
,![]() ,
,
∴当 时,
时,![]() 最大,即点A是最高点,
最大,即点A是最高点,
此时![]() ,
,
∴![]() ;
;
(Ⅲ)∵抛物线经过(-1,0),
∴-1-b+c=0,
∴c=b+1,
∵![]() ,A(0,c)
,A(0,c)
∴![]() , A(0,b+1),
, A(0,b+1),
∴点E关于x轴对称的点![]() ,
,
∵当![]() 满足
满足![]() 值最小时,则此时点P,A,
值最小时,则此时点P,A,![]() 三点共线,
三点共线,
设过点A,P的直线为y=kx+t,将点A(0,b+1),P(1,0)代入得
![]() ,解得:
,解得:![]() ,
,
∴y=(-b-1)x+b+1,
将![]() 代入得:
代入得:![]() ,
,
整理得:![]() ,
,
解得:![]() 或
或![]()
∵b>0,
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】从青岛到济南有南线和北线两条高速公路:南线全长400千米,北线全长320千米.甲、乙两辆客车分别由南线和北线从青岛驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南,求两辆客车从青岛到济南所用的时间是多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
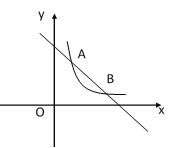
【题目】一次函数y1=kx+b与反比例函数y2=![]() (n>0)交于点A(1,3),B(3,m).
(n>0)交于点A(1,3),B(3,m).
(1)分别求两个函数的解析式;
(2)根据图像直接写出,当x为何值时,y1<y2;
(3)在x轴上找一点P,使得△OAP的面积为6,求出P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
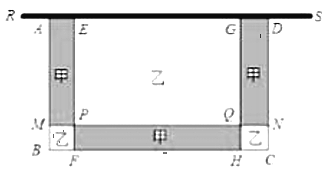
【题目】某校一面墙![]() 前有一块空地,校方准备用长
前有一块空地,校方准备用长![]() 的栅栏(
的栅栏(![]() )围成一个一面靠墙的长方形花围,再将长方形
)围成一个一面靠墙的长方形花围,再将长方形![]() 分割成六块(如图所示) ,已知
分割成六块(如图所示) ,已知![]() ,
,![]() ,
,![]() ,设
,设![]() .
.
(1)用含![]() 的代数式表示:
的代数式表示:![]() ;
;![]() .
.
(2)当长方形![]() 的面积等于
的面积等于![]() 时,求
时,求![]() 的长.
的长.
(3)若在如图的甲区域种植花卉.乙区域种柏草坪,种柏花卉的成本为每平方米100元,种被草坪的成本为每平方米50元,若种植花卉与草坪的总费用超过6300元,求花围的宽![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与直线
与直线![]() 有两个不同的交点.下列结论:①
有两个不同的交点.下列结论:①![]() ;②当
;②当![]() 时,
时,![]() 有最小值
有最小值![]() ;③方程
;③方程![]() 有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则
有两个不等实根;④若连接这两个交点与抛物线的顶点,恰好是一个等腰直角三角形,则![]() ;其中正确的结论的个数是( )
;其中正确的结论的个数是( )
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
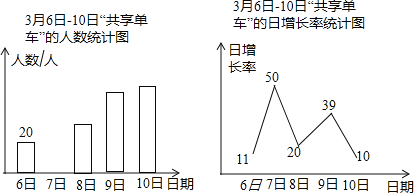
【题目】绿色出行是对环境影响最小的出行方式,“共享单车”已成为北京的一道靓丽的风景线.某社会实践活动小
组为了了解“共享单车”的使用情况,对本校教师在3月6日至3月10日使用单车的情况进行了问卷调查,
以下是根据调查结果绘制的统计图的一部分:
请根据以上信息解答下列问题:
(1)3月7日使用“共享单车”的教师人数为人,并请补全条形统计图;
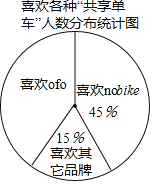
(2)不同品牌的“共享单车”各具特色,社会实践活动小组针对有过使用“共享单车”经历的教师做了进一步调查,每位教师都按要求选择了一种自己喜欢的“共享单车”,统计结果如图,其中喜欢![]() 的教师有36人,求喜欢
的教师有36人,求喜欢![]() 的教师的人数.
的教师的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=1,tan∠CAB=2,将△ABC绕点A旋转后,点B落在AC的延长线上的点D,点C落在点E,DE与直线BC相交于点F,那么CF=_____.
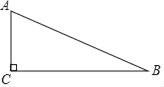
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,以BC为直径的⊙O交AC于点D,过点D作⊙O的切线交AB于点M,交CB延长线于点N,连接OM,OC=1.
(1)求证:AM=MD;
(2)填空:
①若DN![]() ,则△ABC的面积为 ;
,则△ABC的面积为 ;
②当四边形COMD为平行四边形时,∠C的度数为 .
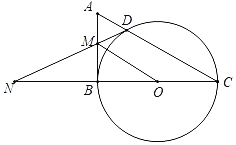
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 的长为半径作
的长为半径作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)填空:
①当四边形![]() 是周长为20的菱形时,
是周长为20的菱形时,![]() ;
;
②当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
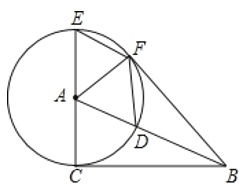
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com