
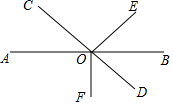
 如图,直线AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数.
如图,直线AB和CD相交于点O,OD平分∠BOF,OE⊥CD于点O,∠AOC=40°,求∠EOF的度数. 科目:初中数学 来源: 题型:选择题
| A. | AB=CD,AD=BC | B. | AB∥CD,AD=BC | C. | AB∥CD,AD∥BC | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{m}$ | B. | $\sqrt{m+2}$ | C. | $\sqrt{{m}^{2}+2}$ | D. | $\sqrt{-20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
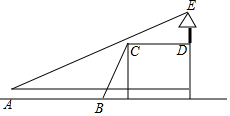 如图,小周站在A处,他的对面有一斜坡BC(坡度i=12:5),现测得小周所站A处到斜坡底端B的距离,AB=15米,坡面BC长为13米.在斜坡顶端C不远处D有一棵树,测得CD=10米,小周看树的顶部E的仰角为30°,此时小周眼睛到地面的高度为1.8米,则数的高度DE约为( )(精确到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)
如图,小周站在A处,他的对面有一斜坡BC(坡度i=12:5),现测得小周所站A处到斜坡底端B的距离,AB=15米,坡面BC长为13米.在斜坡顶端C不远处D有一棵树,测得CD=10米,小周看树的顶部E的仰角为30°,此时小周眼睛到地面的高度为1.8米,则数的高度DE约为( )(精确到1米,$\sqrt{3}$≈1.73,$\sqrt{5}$≈2.24)| A. | 5 | B. | 7 | C. | 12 | D. | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
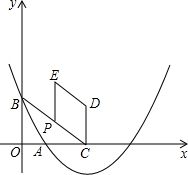 如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.
如图在平面直角坐标系xOy中,抛物线y=$\frac{\sqrt{3}}{5}{x}^{2}$+bx+c过点A(1,0),B(0,$\sqrt{3}$),这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),射线PC绕点P逆时针旋转120°,得线段PE,作平行四边形PCDE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com