
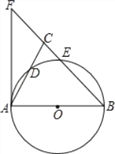
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC、BC于点D、E,延长BC到点F,连接AF,使∠ABC=2∠CAF.
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
【答案】(1)见解析 (2)![]()
【解析】分析:(1)连接BD,由圆周角定理得出∠ADB=90°,由等腰三角形的性质得出∠ABC=2∠ABD,得出∠ABD=∠CAF,证出∠CAF+∠CAB=90°,BA⊥FA,即可得出结论;
(2)连接AE,由圆周角定理得出∠AEB=90°,设CE长为x,则EB长为3x,![]() 由勾股定理可得
由勾股定理可得![]() 在Rt
在Rt![]() 中,由勾股定理得出方程,解方程即可.
中,由勾股定理得出方程,解方程即可.
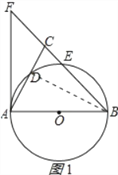
详解:(1)证明:连接BD,如图1所示:
∵AB是⊙O的直径∴∠ADB=90°,
∵BA=BC,
∴BD平分∠ABC,即∠ABC=2∠ABD,
∵∠ABC=2∠CAF,∴∠ABD=∠CAF,
∵∠ABD+∠CAB=90°,
∴∠CAF+∠CAB=90°,即BA⊥FA,
∴AF是⊙O的切线;
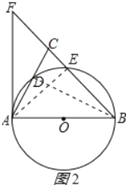
(2)连接AE,如图2所示:
∵AB是⊙O的直径∴∠AEB=90°,即△AEB为直角三角形,
∵![]() 设CE长为x,则EB长为3x,BC长为4x.则AB长为4x,
设CE长为x,则EB长为3x,BC长为4x.则AB长为4x,
在Rt△AEB中由勾股定理可得![]() 在Rt△AEC中,
在Rt△AEC中,![]()
由勾股定理得:![]() ,解得:
,解得:![]()
∵![]()
∴![]()
即CE长为![]()


科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,∠BAD=60°,AC=AD,AC平分∠BAD,M,N分别为AC,CD的中点,BM的延长线交AD于点E,连接MN,BN.对于下列四个结论:①MN∥AD;② BM=MN;③△BAE≌△ACB;④AD=![]() BN,其中正确结论的序号是( )
BN,其中正确结论的序号是( )

A. ①②③④ B. ①②③ C. ①②④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
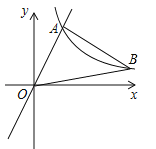
【题目】(2017山东省日照市)如图,在平面直角坐标系中,经过点A的双曲线![]() (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则k的值为______.
,∠AOB=∠OBA=45°,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 都在数轴上,
都在数轴上,![]() 为原点.
为原点.
(1)点![]() 表示的数是 ;
表示的数是 ;
(2)若点![]() 以每秒3个单位长度的速度沿数轴运动,则1秒后点
以每秒3个单位长度的速度沿数轴运动,则1秒后点![]() 表示的数是 ;
表示的数是 ;
(3)若点![]() 都以每秒3个单位长度的速度沿数轴向右运动,而点
都以每秒3个单位长度的速度沿数轴向右运动,而点![]() 不动,
不动,![]() 秒后有一个点是一条线段的中点,求
秒后有一个点是一条线段的中点,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、B、C、D的坐标分别为(-2,2),(一2,1),(3,1),(3,2),线段AD、AB、BC组成的图形记作G,点P沿D-A-B-C移动,设点P移动的距离为a,直线l:y=-x+b过点P,且在点P移动过程中,直线l随点P移动而移动,若直线l过点C,求
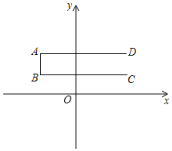
(1)直线l的解析式;
(2)求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观测点A处测得屋顶C与树梢D的仰角分别是45°与60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6米,则树高DE的长度为( )
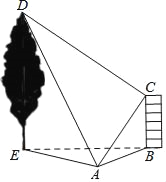
A. 3![]() B. 6
B. 6![]() C. 3
C. 3![]() D. 6
D. 6![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.

(1)如果∠BOC=30°,求∠MON的度数;
(2)如果∠AOB=α,∠BOC=30°,其他条件不变,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一张正方形桌子可坐4人,按图1—图3的方式将桌子拼在一起并安排人员就坐.
(1)两张桌子拼在一起可做 人,三张桌子拼在一起可坐 人,![]() 张桌子拼在一起可坐 人
张桌子拼在一起可坐 人
(2)一家酒楼有60张这样的桌子,按照图1—图3方式每4张拼成一个大桌子,则60张桌子可拼成15张大桌子,共可坐 人
(3)在问题(2)中,若每4张桌子拼成一个大的正方形桌子,则可坐 人
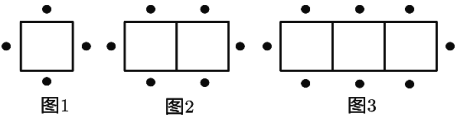
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC的边BC在直线l上,AC⊥BC,且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,且EF=FP(备注:当EF=FP,∠EFP=90°时,∠PEF=∠FPE=45°,反之当∠PEF=∠FPE=45°时,当EF=FP).
(1)在图1中,请你通过观察、测量、猜想并写出AB与AP所满足的数量关系和位置关系.
(2)将△EFP沿直线l向左平移到图2的位置时,EP交AC于点Q,连接AP,BQ.猜想并写出BQ与AP所满足的数量关系和位置关系,并证明你的猜想;
(3)将△EFP沿直线l向左平移到图3的位置时,EP的延长线交AC的延长线于点Q,连接AP、BQ.你认为(2)中所猜想的BQ与AP的结论还成立吗?若成立,给出证明:若不成立,请说明理由.
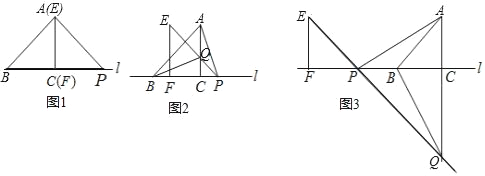
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com