
【题目】在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A=∠B=α∠C;④∠A﹕∠B﹕∠C=1﹕2﹕3中能确定△ABC为直角三角形的条件有( )
A.2个 B.3个 C.4个 D.5个
【答案】A
【解析】
试题分析:结合三角形的内角和为180°逐个分析4个条件,可得出①④中∠C=90°,②③能确定△ABC为锐角三角形,从而得出结论.
解:①∵∠A+∠B=∠C,且∠A+∠B+∠C=180°,
∴∠C+∠C=180°,即∠C=90°,
此时△ABC为直角三角形,①可以;
②∵∠A=∠B=2∠C,且∠A+∠B+∠C=180°,
∴2∠C+2∠C+∠C=180°,
∴∠C=36°,∠A=∠B=2∠C=72°,
△ABC为锐角三角形,②不可以;
③∵∠A=∠B=α∠C,且∠A+∠B+∠C=180°,
∴α∠C+α∠C+∠C=180°,
∴∠C=![]() ,∠A=∠B=α∠C=
,∠A=∠B=α∠C=![]() ,
,
△ABC为锐角三角形,③不可以;
④∵∠A﹕∠B﹕∠C=1﹕2﹕3,
∴∠A+∠B=∠C,同①,
此时△ABC为直角三角形,④可以;
综上可知:①④能确定△ABC为直角三角形.
故选A.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,某计算装置有一数据的入口A和一运算结果的出口B.
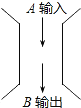
下表是小刚输入一些数后所得的结果:
![]()
(1)若输出的数是5,则小刚输入的数是多少?
(2)若小刚输入的数是225,则输出的结果是多少?
(3)若小刚输入的数是n(n≥10),你能用含n的式子表示输出的结果吗?试一试.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD被直线EF所截,∠1=50°,下列说法错误的是( )
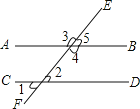
A.如果∠5=50°,那么AB∥CD B.如果∠4=130°,那么AB∥CD
C.如果∠3=130°,那么AB∥CD D.如果∠2=50°,那么AB∥CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为1.第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB,B1C=BC,C1A=CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1,C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=B1C1,C2A1=C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,要使得到的三角形的面积超过2010,最少经过几次操作 ( )

A. 6 B. 5 C. 4 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中正确的有( )个
①三个内角对应相等的两个三角形全等;
②三条边对应相等的两个三角形全等;
③有两角和一边分别对应相等的两个三角形全等;
④等底等高的两个三角形全等.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,∠COD=90°,直线AB与OC交于点B,与OD交于点A,射线OE和射线AF交于点G.

(1)若OE平分∠BOA,AF平分∠BAD,∠OBA=30°,则∠OGA=
(2)若∠GOA=![]() ∠BOA,∠GAD=
∠BOA,∠GAD=![]() ∠BAD,∠OBA=30°,则∠OGA=
∠BAD,∠OBA=30°,则∠OGA=
(3)将(2)中“∠OBA=30°”改为“∠OBA=α”,其余条件不变,则∠OGA= (用含α的代数式表示)
(4)若OE将∠BOA分成1:2两部分,AF平分∠BAD,∠ABO=α(30°<α<90°),求∠OGA的度数(用含α的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮和小刚进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的1.5倍.设两人出发x min后距出发点的距离为y m.图中折线表示小亮在整个训练中y与x的函数关系,其中A点在x轴上,M点坐标为(2,0).

(1)A点所表示的实际意义是 ;![]() = ;
= ;
(2)求出AB所在直线的函数关系式;
(3)如果小刚上坡平均速度是小亮上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com