
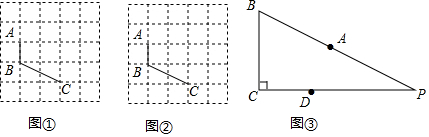
分析 (1)根据对等四边形的定义,进行画图即可;
(2)根据对等四边形的定义,分两种情况:①若CD=AB,此时点D在D1的位置,CD1=AB=$\frac{13}{2}$;②若AD=BC,此时点D在D2、D3的位置,AD2=AD3=BC=5;利用勾股定理和矩形的性质,求出相关相关线段的长度,即可解答.
解答 解:(1)如图①②所示,四边形ABCD即为所求;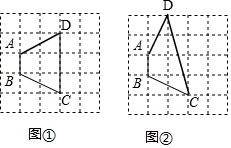
(2)如图③所示,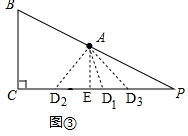
当AB=CD时,此时点D位于D1位置,CD1=AB=$\frac{1}{2}$BP=$\frac{13}{2}$;
当BC=AD=5时,此时点D位于D2、D3位置,
过点A作AE⊥PC,
则AE为△PBC的中位线,
∴AE=$\frac{1}{2}$BC=$\frac{5}{2}$,CE=$\frac{1}{2}$PC=6,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{{5}^{2}-(\frac{5}{2})^{2}}$=$\frac{5\sqrt{3}}{2}$,
∴CD=6+$\frac{5\sqrt{3}}{2}$或6-$\frac{5\sqrt{3}}{2}$,
故答案为:$\frac{13}{2}$或6+$\frac{5\sqrt{3}}{2}$或6-$\frac{5\sqrt{3}}{2}$.
点评 题主要考查了四边形的综合题,解题的关键是理解并能运用“等对边四边形”这个概念.在(3)中注意分类讨论思想的应用、勾股定理的应用.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:解答题
 在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
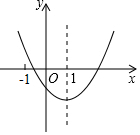 如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )
如图是二次函数y=ax2+bx+c的图象,其对称轴为直线x=1,则下列结论错误的是( )| A. | a>0 | |
| B. | 2a+b=0 | |
| C. | a-b+c<0 | |
| D. | 若($\frac{1}{2}$,y1),(3,y2)是抛物线上两点,则y1<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com