D
分析:判定两三角形全等的方法有四种:SSS,SAS,ASA,AAS,要得到△AOC≌△BOC中已有∠1=∠2,还有CO为公共边,若加A选项的条件,就可根据“ASA”来判定;若加B选项条件,可根据“AAS”来判定;若加C选项条件,可根据“SAS”来判定;若加上D选项,不满足上述全等的方法,从而得到正确的选项.
解答:若加上∠3=∠4,
在△AOC和△BOC中,
∠1=∠2,OC=OC,∠3=∠4,
∴△AOC≌△BOC,故选项A能判定;
若加上∠A=∠B,
在△AOC和△BOC中,
∠1=∠2,∠A=∠B,OC=OC
∴△AOC≌△BOC,故选项B能判定;
若加上AO=BO,
在△AOC和△BOC中,
AO=BO,∠1=∠2,OC=OC,
∴△AOC≌△BOC,故选项C能判定;
若加上AC=BC,
则已有的条件为两边及其中一边的对角对应相等,不满足全等的判定方法,
所以不能判定出△AOC和△BOC全等,故选项D不能判定.
故选D
点评:此题属于条件开放型试题,重在考查学生全等三角形的判定,解答这类试题,需要执果索因,逆向思维,逐步探求使结论成立的条件.解决这类问题还要注意挖掘图形中的隐含条件,如公共边、对顶角相等、公共角等.

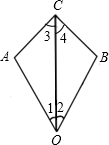 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△AOC≌△BOC的是
如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△AOC≌△BOC的是

 =2,∠ADC=30°
=2,∠ADC=30°