
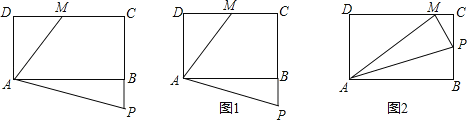
【题目】如图,矩形ABCD(AB>AD)中,点M是边DC上的一点,点P是射线CB上的动点,连接AM,AP,且∠DAP=2∠AMD.
(1)若∠APC=76°,则∠DAM= ;
(2)猜想∠APC与∠DAM的数量关系为 ,并进行证明;
(3)如图1,若点M为DC的中点,求证:2AD=BP+AP;
(4)如图2,当∠AMP=∠APM时,若CP=15,![]() =
=![]() 时,则线段MC的长为 .
时,则线段MC的长为 .
【答案】(1)38°;(2)∠APC=2∠DAM,证明见解析;(3)见解析;(4)3![]() .
.
【解析】
(1)由AD∥CP,∠APC=76°知∠DAP=104°,根据∠DAP=2∠AMD得∠AMD=52°,结合∠D=90°可得;
(2)由AD∥CP知∠DAP+∠APC=180°,结合∠DAP=2∠AMD得2∠AMD+∠APC=180°,再结合∠D=90°知∠AMD=90°﹣∠DAM,即2(90°﹣∠DAM)+∠APC=180°,据此可得;
(3)延长AM交BC的延长线于点E,延长BP到F,使PF=AP,连接AF,证△AMD≌△EMC得AD=CE,据此知BE=BC+CE=2AD,再证∠E=∠F得AE=AF,由AB⊥BE知BE=BF,从而由BF=BP+PF=BP+AP可得;
(4)延长MD到点E,使DE=MD,连接AE,作EF⊥MA,设AM=3x,则AD=2x,DM=DE![]() x,AE=AP=3x,证△ADM∽△EFM得
x,AE=AP=3x,证△ADM∽△EFM得![]() ,求得EF
,求得EF![]() x,AF
x,AF![]() x,再证△EAF≌△APB得PB=AF
x,再证△EAF≌△APB得PB=AF![]() x,再由AD=BC得
x,再由AD=BC得![]() x+15=2x,求得x的值,从而得出AB的长,根据MC=DC﹣DM=AB﹣DM可得答案.
x+15=2x,求得x的值,从而得出AB的长,根据MC=DC﹣DM=AB﹣DM可得答案.
(1)∵AD∥CP,∠APC=76°,
∴∠DAP=104°.
∵∠DAP=2∠AMD,
∴∠AMD=52°,
又∵∠D=90°,
∴∠DAM=38°.
故答案为:38°;
(2)∠APC=2∠DAM.理由如下:
∵四边形ABCD是矩形,
∴∠D=90°,AD∥BC.
∵点P是射线CB上的点,
∴AD∥CP,
∴∠DAP+∠APC=180°.
∵∠DAP=2∠AMD,
∴2∠AMD+∠APC=180°,
在Rt△AMD中,∠D=90°,
∴∠AMD=90°﹣∠DAM,
∴2(90°﹣∠DAM)+∠APC=180°,
∴∠APC=2∠DAM.
故答案为:∠APC=2∠DAM;
(3)如图1,延长AM交BC的延长线于点E,延长BP到F,使PF=AP,连接AF,
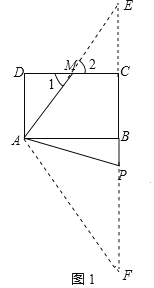
∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,∠ABC=90°,
∴AD∥BE,AB⊥BE,
∴∠DAM=∠E.
∵M是DC中点,
∴DM=CM,
又∵∠1=∠2,
∴△AMD≌△EMC(AAS),
∴AD=CE,
∴BE=BC+CE=2AD.
∵∠APC=2∠DAM,
∴∠APC=2∠E.
∵PA=PF,
∴∠PAF=∠F,
∴∠APC=2∠F,
∴∠E=∠F,
∴AE=AF,
又∵AB⊥BE,
∴BE=BF,
又∵BF=BP+PF=BP+AP,
∴2AD=BP+AP;
(4)如图2,延长MD到点E,使DE=MD,连接AE,过点E作EF⊥MA于点F,
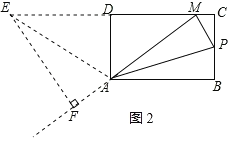
设AM=3x,则AD=2x,DM=DE![]() x,AE=AP=3x.
x,AE=AP=3x.
∵∠AMD=∠EMF,∠ADM=∠EFM=90°,
∴△ADM∽△EFM,
∴![]() ,即
,即![]() ,
,
解得:EF![]() x,
x,
∴AF![]() x.
x.
∵DE=MD,AD⊥CE,
∴∠AME=∠AEM,
则∠EAF=2∠AMD.
∵AD∥BC,∠DAP=2∠AMD,
∴∠APB=∠DAP=2∠AMD,
∴∠EAF=∠APB,
又∵∠EFA=∠B=90°,AE=AP,
∴△EAF≌△APB(AAS),
∴PB=AF![]() x,
x,
由AD=BC得![]() x+15=2x,
x+15=2x,
解得:x=9,
∴AB![]() 12
12![]() ,
,
∴MC=DC﹣DM=AB﹣DM=![]() =3
=3![]() .
.
故答案为:3![]() .
.


科目:初中数学 来源: 题型:
【题目】已知一张正方形ABCD纸片,边长AB=2,按步骤进行折叠,如图1,先将正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
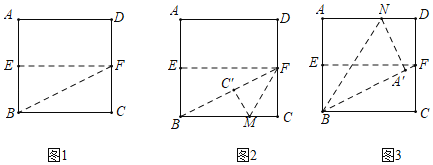
(1)如图2,将CF边折到BF上,得到折痕FM,点C的对应点为C',求CM的长.
(2)如图3,将AB边折到BF上,得到折痕BN,点A的对应点为A',求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”、“戏剧”、“散文”、“其他”四个类别,每位同学仅选一项,根据调查结果绘制了不完整的频数分布表和扇形统计图.根据图表提供的信息,回答下列问题:
类别 | 频数(人数) | 频率 |
小说 | 0.5 | |
戏剧 | 4 | |
散文 | 10 | 0.25 |
其他 | 6 | |
合计 | m | 1 |
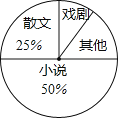
(1)计算m= ;
(2)在扇形统计图中,“其他”类所占的百分比为 ;
(3)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从中任意选出2名同学参加学校的戏剧社团,请用画树状图或列表的方法,求选取的2人恰好是乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
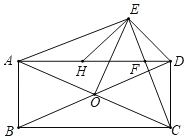
【题目】如图,在ABCD中,对角线AC,BD相交于点O,以AC为斜边的等腰直角三角形AEC的边CE,与AD交于点F,连接OE,使得OE=OD.在AD上截取AH=CD,连接EH,ED.
(1)判断四边形ABCD的形状,并说明理由;
(2)若AB=1,BC=3,求EH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有4张看上去无差别的卡片,上面分别写着1,2,3,4.
(1)一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;
(2)随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受到“新型肺炎”影响,全国中小学未能按时开学,为响应国家“停课不停学”的号召,重庆某重点中学组织全校师生开展线上教学活动,体育备课组也为同学们提出了每日锻炼建议.疫情过去开学后,体育组彭老师为检测同学们在家锻炼情况,在甲、乙两班同学中各随机抽取![]() 名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
名学生进行检测,并对数据进行了整理、分析.下面给出了部分信息:
甲班![]()
乙班成绩在![]() 中的数据是
中的数据是![]()
整理数据:
成绩 班级 |
|
|
|
|
甲 |
|
|
|
|
乙 |
|
|
|
|
分析数据:
班级 | 平均数 | 中位数 | 众数 |
甲 |
|
|
|
乙 |
|
|
|
根据以上信息,回答下列问题:
![]()
![]()
![]()
![]()
![]() 根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(
根据以上数据,你认为哪个班级在家体育锻炼的效果比较好,请说明理由(![]() 条理由即可).
条理由即可).
![]() 已知九年级共有
已知九年级共有![]() 名学生,请估计全年级体育成绩大于等于
名学生,请估计全年级体育成绩大于等于![]() 分的学生有多少人?
分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c经过(﹣1,0),(0,﹣3),(2,3)三点.
(1)求这条抛物线的表达式;
(2)写出抛物线的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
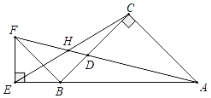
【题目】如图,点A、B、E在同一直线上,∠FEB=∠ACB=90°,AC=BC,EB=EF,连AF,CE交于点H,AF、CB交于点D,若tan∠CAD=![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com