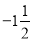练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    的倒数是__________，绝对值等于的数是__________．

    ±10 【解析】试题解析：∵， 的倒数是， ∴的倒数为， ∵， ∴. 故答案为： ，±10.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：云南省双柏县2017-2018学年八年级上期期末数学试卷 题型：填空题

    计算： =___________________．

    -1 【解析】【解析】 原式=．故答案为：－1．

    查看答案和解析>>

    科目：初中数学 来源：山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型：填空题

    如图，抛物线y=ax2+bx+c（a＞0）的对称轴是过点（1，0）且平行于y轴的直线，若点P（4，0）在该抛物线上，则4a﹣2b+c的值为_________．

    0 【解析】试题分析：设抛物线与x轴的另一个交点是Q，∵抛物线的对称轴是过点（1，0），与x轴的一个交点是P（4，0），∴与x轴的另一个交点Q（﹣2，0），把（﹣2，0）代入解析式得：0=4a﹣2b+c，∴4a﹣2b+c=0，故答案为：0．

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：解答题

    如图，一只甲虫在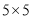的方格(每小格边长为)上沿着网格线运动，网格线与网格线的交点为格点，甲虫从处出发去看望格点、、处的其它甲虫，若规定：向上向右走均为正，向下向左走均为负，如果从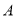到记为： ，从到记为： ，其中第一个数表示左右方向，第二个数表示上下方向．

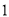    （）图中__________；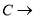

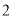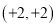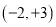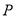    （）若这只甲虫从处出发，行走路线依次为， ， ， ，最后在点停止运动，请在图中标出点的位置；

    （）若这只甲虫的行走路线为，则该甲虫走过的路程长度为__________；

    （）若图中另有两个格点、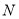，且， ，则应记为__________．

    （）；（）图形见解析；（）；（）应记为 【解析】试题分析：（1）根据规定及实例可知：C→D记为（+1，-2）； （2）按题目所示平移规律分别向右向上平移2个格点，再向右平移2个格点，向下平移1个格点；向左平移2个格点，向上平移3个格点；向左平移1个向下平移两个格点即可得到点P的坐标，在图中标出即可； （3）分别根据各点的坐标计算总长即可； （4）令M→A与M→N对应的横纵坐标相...

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：填空题

    若，则的值为__________．

    1 【解析】试题解析：∵， ∴， ∴． 故答案为1.

    查看答案和解析>>

    科目：初中数学 来源：北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型：单选题

    在下列各数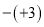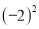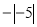， ， ， ， 中，负数有（ ）．

    A. 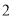个 B. 个 C. 个 D. 个

    B 【解析】试题解析： ， ， ， ， ． ∴负数有个． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：天津市2018届九年级（上）第四周周清数学试卷 题型：解答题

    已知二次函数的图象与x轴的两个交点坐标是（﹣3，0）和（4，0），这个函数也过点（6，18），求这个二次函数的解析式．

    y=x2﹣x﹣12 【解析】试题分析：设二次函数的解析式为y=ax2+bx+c（a≠0），再把函数的图象与x轴的两个交点坐标以及点（6，18）代入求出a，b，c的值即可． 试题解析：设二次函数的解析式为y=ax2+bx+c（a≠0）． 根据题意，得， 解得： ， ∴二次函数的解析式为y=x2﹣x﹣12．

    查看答案和解析>>

    科目：初中数学 来源：广东省广州市天河区2017-2018学年八年级上学期期末考试数学试卷 题型：解答题

    如图，△ABC中，AB=AC，作AD⊥BC，CE⊥AB，垂足分别为D，E，AD和CE相交于点F，若已知AE=CE.

    (1)求证：△AEF≌△CEB；

    (2)求证：AF=2CD

    （1）证明见解析；（2）证明见解析. 【解析】试题分析：（1）要证明△AEF≌△CEB，已知条件有AE=EC，∠AEF=∠BEC=90°，还差一个条件，由AD⊥BC，CE⊥AB可得∠B+∠BAD=90°，∠B+∠BCE=90°，所以得出∠EAF=∠ECB，因此可证明出△AEF≌△CEB；（2）由（1）结论可得：AF=BC，即要证明BC=2CD，由等腰三角形三线合一性质不难证明. 试题解...

    查看答案和解析>>

    科目：初中数学 来源：江苏省东部分校2017-2018学年八年级上学期期末考试数学试卷 题型：单选题

    已知无论n取什么实数，点P（n, 4n-3）都在直线l上，若Q（a， b）是直线l上的点，则4a-b的平方根等于（　　）

    A. B. 1 C. D.

    D 【解析】试题解析：∵令n=0，则P（0，-3）；再令n=1，则P（1，1），由于n不论为何值此点均在直线l上， ∴设此直线的解析式为y=kx+b（k≠0）， ∴， 解得， ∴此直线的解析式为：y=4x-3， ∵Q（a，b）是直线l上的点， ∴4a-3=b，即4a-b=3， ∴4a-b的平方根等于 故选D.

    查看答案和解析>>

    同步练习册答案