
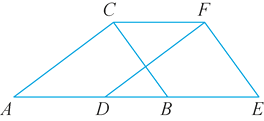
【题目】如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=![]() ,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).
,抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6).
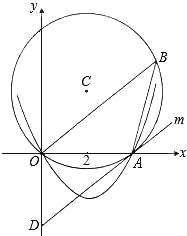
(1)求抛物线的函数解析式;
(2)直线m与⊙C相切于点A,交y轴于点D.动点P在线段OB上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动;点P的速度为每秒一个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值;
(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.
【答案】(1) y=![]() x2﹣2x.(2) t=1.8秒;(3) R(
x2﹣2x.(2) t=1.8秒;(3) R(![]() ,
,![]() ).
).
【解析】
试题分析:(1)根据抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),利用待定系数法求抛物线解析式;
(2)如图1,由已知条件,可以计算出OD、AE等线段的长度.当PQ⊥AD时,过点O作OF⊥AD于点F,此时四边形OFQP、OFAE均为矩形.则在Rt△ODF中,利用勾股定理求出DF的长度,从而得到时间t的数值;
(3)因为OB为定值,欲使△ROB面积最大,只需OB边上的高最大即可.按照这个思路解决本题.
如图2,当直线l平行于OB,且与抛物线相切时,OB边上的高最大,从而△ROB的面积最大.联立直线l和抛物线的解析式,利用一元二次方程判别式等于0的结论可以求出R点的坐标.
试题解析:(1)∵抛物线y=ax2+bx经过点A(4,0)与点(﹣2,6),
∴![]() ,
,
解得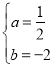
∴抛物线的解析式为:y=![]() x2﹣2x.
x2﹣2x.
(2)如图1,连接AC交OB于点E,由垂径定理得AC⊥OB.
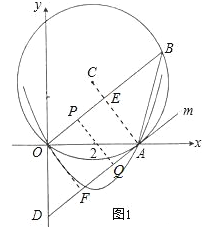
∵AD为切线,
∴AC⊥AD,
∴AD∥OB.
过O点作OF⊥AD于F,
∴四边形OFAE是矩形,
∵tan∠AOB=![]() ,
,
∴sin∠AOB=![]() ,
,
∴AE=OAsin∠AOB=4×![]() =2.4,
=2.4,
OD=OAtan∠OAD=OAtan∠AOB=4×![]() =3.
=3.
当PQ⊥AD时,OP=t,DQ=2t.
在Rt△ODF中,
∵OD=3,OF=AE=2.4,DF=DQ﹣FQ=DQ﹣OP=2t﹣t=t,
由勾股定理得:DF=![]() ,
,
∴t=1.8秒;
(3)如图2,设直线l平行于OB,且与抛物线有唯一交点R(相切),
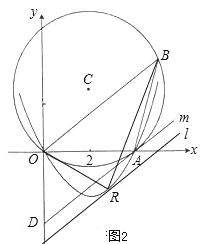
此时△ROB中OB边上的高最大,所以此时△ROB面积最大.
∵tan∠AOB=![]() ,∴直线OB的解析式为y=
,∴直线OB的解析式为y=![]() x,
x,
由直线l平行于OB,可设直线l解析式为y=![]() x+b.
x+b.
∵点R既在直线l上,又在抛物线上,
∴![]() x2﹣2x=
x2﹣2x=![]() x+b,化简得:2x2﹣11x﹣4b=0.
x+b,化简得:2x2﹣11x﹣4b=0.
∵直线l与抛物线有唯一交点R(相切),
∴判别式△=0,即112+32b=0,解得b=﹣![]() ,
,
此时原方程的解为x=![]() ,即xR=
,即xR=![]() ,
,
而yR=![]() xR2﹣2xR=
xR2﹣2xR=![]()
∴点R的坐标为R(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】一台收割机工作效率相当于一个农民工作效率的150倍,用这台机器收割10公顷小麦比100个农民人工收割这些小麦要少用1小时,这台收割每小时收割多少公顷小麦?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年春节我市共接待国内外游客总人数3343200万人次,3343200这个数用科学记数法表示为( )
A. 0.33432×106 B. 3.3432×106 C. 3.3432×105 D. 33.432×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】芝麻作为食品和药物,均广泛使用.经测算,一粒芝麻约有0.00000201千克,用科学记数法表示为( )
A. 2.01×10-6千克 B. 0.201×10-5千克 C. 20.1×10-7千克 D. 2.01×10-7千克
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的有( ):①单项式必须是同类项才能相乘;②几个单项式的积,仍是单项式;③几个单项式之和仍是单项式;④几个单项式相乘,有一个因式为0,积一定为0.
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将二次函数y=x2的图象向下平移一个单位,则平移以后的二次函数的解析式为( )
A.y=x2-1 B.y=x2+1
C.y=(x-1)2 D.y=(x+1)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,∠A=33°,将三角形ABC沿AB方向向右平移得到三角形DEF.
(1)试求出∠E的度数;
(2)若AE=9 cm,DB=2 cm,求出BE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com